Tangentna ravnina. Tangentna ravnina in normala površine

Tangentne ravnine igrajo veliko vlogo v geometriji. Konstrukcija tangentnih ravnin je v praktičnem smislu pomembna, saj njihova prisotnost omogoča določitev smeri normale na površino na točki stika. Ta problem se pogosto uporablja v inženirski praksi. Tangentne ravnine se uporabljajo tudi za izdelavo skic geometrijskih likov, omejenih z zaprtimi površinami. V teoretičnem smislu se ravnine, ki se dotikajo površine, uporabljajo v diferencialni geometriji za preučevanje lastnosti površine v območju tangentne točke.

Osnovni pojmi in definicije

Ravnino, ki se dotika površine, je treba obravnavati kot mejni položaj sekantne ravnine (podobno kot premica, ki se dotika krivulje, ki je prav tako definirana kot mejni položaj sekante).

Ravnina, ki se dotika ploskve v dani točki na ploskvi, je množica vseh premic – tangent, ki potekajo na ploskev skozi dano točko.

V diferencialni geometriji je dokazano, da so vse tangente na ploskev, narisane v navadni točki, komplanarne (pripadajo isti ravnini).

Ugotovimo, kako je narisana ravna črta, ki se dotika površine. Tangenta t na ploskev β v točki M, podani na ploskvi (sl. 203), predstavlja mejni položaj sekante l j, ki seka ploskev v dveh točkah (MM 1, MM 2, ..., MM n), ko presečišča sovpadata (M ≡ M n , l n ≡ l M). Očitno je (M 1 , M 2 , ..., M n ) ∈ g, saj je g ⊂ β. Iz zgornjega izhaja naslednja definicija: tangenta na površino je premica, ki se dotika katere koli krivulje, ki pripada površini.

Ker je ravnina določena z dvema sekajočima se ravnima črtama, je za določitev ravnine tangente na površino v dani točki dovolj, da skozi to točko narišemo dve poljubni črti, ki pripadata površini (po možnosti preproste oblike), in zgradimo tangente na vsaka od njih na presečišču teh črt. Konstruirane tangente enolično določajo tangentno ravnino. Vizualni prikaz držanja ravnine α, tangentne na površino β v dani točki M, je podan na sl. 204. Ta slika prikazuje tudi normalo n na površino β.

Normala na površino v dani točki je premica, ki je pravokotna na tangentno ravnino in poteka skozi stično točko.

Presek površja z ravnino, ki poteka skozi normalo, imenujemo normalni prerez površja. Odvisno od vrste ploskve ima lahko tangentna ravnina s ploskvijo eno ali več točk (premic). Stična črta je lahko hkrati tudi presečišče ploskve z ravnino.

Obstajajo tudi primeri, ko so na površini točke, kjer ni mogoče narisati tangente na površino; take točke imenujemo singularne. Kot primer singularnih točk lahko navedemo točke, ki pripadajo vrhunskemu robu ploskve trupa, ali točko presečišča poldnevnika vrtilne ploskve z njeno osjo, če se poldnevnik in os ne sekata desno kota.

Vrste stika so odvisne od narave ukrivljenosti površine.

ukrivljenost površine

Probleme površinske ukrivljenosti je raziskoval francoski matematik F. Dupin (1784-1873), ki je predlagal vizualni način prikazovanja sprememb ukrivljenosti normalnih odsekov površine.

Da bi to naredili, so v ravnini, tangentni na obravnavano površino v točki M (sl. 205, 206), na tangentah normalnih odsekov na obeh straneh te točke narisani segmenti, ki so enaki kvadratnim korenom vrednosti ustrezne polmere ukrivljenosti teh odsekov. Množica točk – koncev segmentov določa krivuljo, imenovano Dupinova indikatrisa. Algoritem za konstrukcijo Dupinove indikatrise (slika 205) lahko zapišemo:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(R l 1), = √(R l 2),..., = √(R l n)

kjer je R polmer ukrivljenosti.

(A 1 ∪ A 2 ∪ ... ∪ A n) je Dupinova indikatrisa.

Če je Dupinova indikatrisa ploskve elipsa, se točka M imenuje eliptična, ploskev pa ploskev z eliptičnimi točkami.(Slika 206). V tem primeru ima tangentna ravnina samo eno skupno točko s površino in vse črte, ki pripadajo površini in se sekajo v obravnavani točki, se nahajajo na isti strani tangentne ravnine. Primeri površin z eliptičnimi točkami so: vrtilni paraboloid, vrtilni elipsoid, krogla (v tem primeru je Dupinova indikatrisa krog itd.).

Pri risanju tangentne ravnine na ploskev trupa se bo ravnina dotikala te ploskve vzdolž ravne generatrise. Točke te premice imenujemo parabolična, površina pa je ploskev s paraboličnimi točkami. Dupinova indikatrisa sta v tem primeru dve vzporedni premici (slika 207*).

Na sl. 208 prikazuje površino, sestavljeno iz točk, v katerih

* Krivulja drugega reda - parabola - lahko pod določenimi pogoji razpade na dve realni vzporedni črti, dve namišljeni vzporedni črti, dve sovpadajoči črti. Na sl. 207 imamo opraviti z dvema pravima vzporednima premicama.

Ohlapna tangentna ravnina seka površino. Takšna površina se imenuje hiperbolično, in točke, ki mu pripadajo - hiperbolične točke. Dupinova indikatrisa je v tem primeru hiperbola.

Površina, katere vse točke so hiperbolične, ima obliko sedla (poševna ravnina, enolistni hiperboloid, konkavne ploskve revolucije itd.).

Ena površina ima lahko točke različnih tipov, na primer na površini trupa (slika 209) je točka M eliptična; točka N - parabolična; točka K je hiperbolična.

V okviru diferencialne geometrije je dokazano, da imajo normalni odseki, v katerih so vrednosti ukrivljenosti K j = 1/ R j (kjer je R j polmer ukrivljenosti obravnavanega odseka), ekstremne vrednosti, ki se nahajajo v dve med seboj pravokotni ravnini.

Takšne ukrivljenosti K 1 = 1/R max. K 2 \u003d 1 / R min se imenujejo glavne, vrednosti H \u003d (K 1 + K 2) / 2 in K \u003d K 1 K 2 - povprečna ukrivljenost površino in celotno (Gaussovo) ukrivljenost površine v obravnavani točki. Za eliptične točke K > 0, hiperbolično K

Nastavitev ravnine tangente na površino na Mongeovem diagramu

V nadaljevanju bomo na konkretnih primerih prikazali konstrukcijo ravnine, tangentne na površino z eliptičnimi (primer 1), paraboličnimi (primer 2) in hiperboličnimi (primer 3) točkami.

PRIMER 1. Konstruirajte ravnino α, tangentno na vrtilno površino β, z eliptičnimi točkami. Razmislite o dveh možnostih za rešitev tega problema, a) točka M ∈ β in b) točka M ∉ β

Možnost a (slika 210).

Tangentna ravnina je določena z dvema tangentama t 1 in t 2, narisanima v točki M na vzporednik in poldnevnik površine β.

Projekcije tangente t 1 na vzporednik h površine β bodo t" 1 ⊥ (S"M") in t" 1 || x os. Vodoravna projekcija tangente t "2 na poldnevnik d površine β, ki poteka skozi točko M, bo sovpadala z vodoravno projekcijo poldnevnika. Če želite najti čelno projekcijo tangente t" 2, meridionalna ravnina γ (γ ∋ M) z vrtenjem okoli osi ploskve β prestavimo v lego γ 1 vzporedno z ravnino π 2 . V tem primeru je točka M → M 1 (M "1, M" 1). Projekcija tangente t "2 rarr; t" 2 1 je določena z (M "1 S"). Če zdaj ravnino γ 1 vrnemo v prvotni položaj, bo točka S "ostala na svojem mestu (kot pripadajoča vrtilni osi), M" 1 → M "in čelna projekcija tangente t" 2 bosta biti odločen (M "S")

Dve tangenti t 1 in t 2, ki se sekata v točki M ∈ β, določata ravnino α, ki se dotika površine β.

Možnost b (slika 211)

Za konstruiranje ravnine, ki se dotika površine, ki poteka skozi točko, ki ne pripada površini, je treba izhajati iz naslednjih premislekov: skozi točko zunaj površine, sestavljeno iz eliptičnih točk, lahko narišemo veliko ravnin, ki se dotikajo površine. Ovojnica teh ploskev bo neka stožčasta ploskev. Torej, če ni dodatnih indikacij, ima problem veliko rešitev in se v tem primeru zmanjša na risanje stožčaste površine γ, ki se dotika dane površine β.

Na sl. 211 prikazuje konstrukcijo stožčaste ploskve γ, ki se dotika krogle β. Vsaka ravnina α, ki se dotika stožčaste površine γ, bo tangentna na površino β.

Za izdelavo projekcij površine γ iz točk M "in M" narišemo tangente na kroge h "in f" - projekcije krogle. Označite točke dotika 1 (1" in 1"), 2 (2" in 2"), 3 (3" in 3") in 4 (4" in 4"). Horizontalna projekcija kroga - stična črta med stožčasto površino in kroglo bo projicirana v [ 1"2"] Da bi našli točke elipse, v katere je ta krog projiciran na čelno ravnino projekcij, bomo uporabite vzporednice krogle.

Na sl. 211 na ta način določimo čelni projekciji točk E in F (E "in F"). Če imamo stožčasto ploskev γ, nanjo konstruiramo tangentno ravnino α. Narava in zaporedje grafike

Nekatere konstrukcije, ki jih je treba narediti za to, so prikazane v naslednjem primeru.

PRIMER 2 Konstruirajte ravnino α, ki se dotika ploskve β s paraboličnimi točkami

Tako kot v primeru 1 upoštevajmo dve rešitvi: a) točko N ∈ β; b) točka N ∉ β

Možnost a (riž 212).

Stožčasta ploskev se nanaša na ploskve s paraboličnimi točkami (glej sliko 207.) Ravnina, ki je tangentna na stožčasto ploskev, se le-te dotika vzdolž premočrtne generatrise.Če želite jo zgraditi, morate:

1) narišite generatriko SN (S"N" in S"N") skozi dano točko N;

2) označimo presečišče generatrise (SN) z vodilom d: (SN) ∩ d = A;

3) nariši in tangento t na d v točki A.

Generatrisa (SA) in tangenta t, ki jo seka, določata ravnino α, ki se dotika stožčaste ploskve β v dani točki N*.

Narisati ravnino α, ki se dotika stožčaste površine β in poteka skozi točko N, ne pripada

* Ker je ploskev β sestavljena iz paraboličnih točk (razen oglišča S), ravnina α, ki se dotika nanjo, ne bo imela skupne točke N, temveč premico (SN).

s pritiskom na določeno površino je potrebno:

1) skozi dano točko N in oglišče S stožčaste površine β narišite ravno črto a (a "in a");

2) določi vodoravno sled te premice H a ;

3) narišite tangenti t "1 in t" 2 krivulje h 0β skozi H a - vodoravno sled stožčaste površine;

4) povežite tangentni točki A (A "in A") in B (B "in B") na vrh stožčaste površine S (S "in S").

Sekajoči premici t 1 , (AS) in t 2 , (BS) določata želeni tangentni ravnini α 1 in α 2

PRIMER 3. Konstruirajte ravnino α, ki se dotika ploskve β s hiperboličnimi točkami.

Točka K (slika 214) se nahaja na površini globoida (notranja površina obroča).

Za določitev položaja tangentne ravnine α je potrebno:

1) skozi točko K potegnemo vzporednico s površino β h(h", h");

2) narišite tangento skozi točko K" t" 1 (t" 1 ≡ h");

3) za določitev smeri projekcij tangente na meridionalni odsek je potrebno narisati ravnino γ skozi točko K in os površine, vodoravna projekcija t "2 bo sovpadala s h 0γ; konstruirati čelno projekcijo tangente t" 2 najprej translatiramo ravnino γ z vrtenjem okoli osi vrtilne ploskve v položaj γ 1 || π 2 . V tem primeru bo meridionalni odsek z ravnino γ sovpadal z levim obrisnim lokom čelne projekcije - polkrogom g".

Točka K (K", K"), ki pripada krivulji meridianskega odseka, se premakne v položaj K 1 (K "1, K" 1). Skozi K" 1 narišemo čelno projekcijo tangente t" 2 1, poravnano z ravnino γ 1 || π 2 in označite točko njegovega presečišča s čelno projekcijo osi vrtenja S "1. Ravnino γ 1 vrnemo v prvotni položaj, točko K" 1 → K "(točka S" 1 ≡ S ") Čelno projekcijo tangente t" 2 določata točki K" in S".

Tangenti t 1 in t 2 določata želeno tangentno ravnino α, ki seka ploskev β po krivulji l .

PRIMER 4. Konstruirajte ravnino α, ki se dotika ploskve β v točki K. Točka K se nahaja na ploskvi enolistnega vrtilnega hiperboloida (slika 215).

Ta problem je mogoče rešiti tako, da sledimo algoritmu, uporabljenemu v prejšnjem primeru, vendar ob upoštevanju, da je površina enolistnega vrtilnega hiperboloida linijasta površina, ki ima dve družini premočrtnih generatorjev in vsak od generatorjev ene družine seka vse generatorje druge družine (glej § 32, slika 138). Skozi vsako točko te ploskve lahko narišemo dve sekajoči se ravni črti - generatorji, ki se bosta hkrati dotikali ploskve enolistnega vrtilnega hiperboloida.

Te tangente določajo tangentno ravnino, tj. ravnina, ki se dotika površine enolistnega vrtilnega hiperboloida, seka to ploskev po dveh premicah g 1 in g 2 . Če želite zgraditi projekcije teh črt, je dovolj, da uporabite vodoravno projekcijo točke K, da prenesete tangente t "1 in t" 2 na vodoravno

talna projekcija kroga d "2 - grlo površine enolistnega vrtilnega hiperboloida; določite točki 1" in 2, na katerih t "1 in t" 2 sekata eno od površinskih vodil d 1. Iz 1" in 2" najdemo 1" in 2", ki skupaj s K" določata čelne projekcije želenih črt.

Prenesite iz Depositfiles

4. TEORIJA POVRŠIN.

4.1 ENAČBE POVRŠIN.

Površino v 3D prostoru lahko definiramo:

1) implicitno: F ( x , l , z ) =0 (4.1)

2) izrecno: z = f ( x , l ) (4.2)

3) parametrično: (4.3)

ali:
(4.3’)

kje so skalarni argumenti
včasih imenovane krivuljne koordinate. Na primer, krogla
priročno je nastaviti v sferičnih koordinatah:
.

4.2 TANGENTNA RAVNINA IN NORMALNA NA POVRŠJE.

Če premica leži na površini (4.1), potem koordinate njenih točk izpolnjujejo enačbo površine:

Če razlikujemo to identiteto, dobimo:

(4.4)

oz
(4.4 ’ )

na vsaki točki krivulje na površini. Tako je gradientni vektor na nesingularnih točkah površine (kjer je funkcija (4.5) diferenciabilna in
) je pravokotna na tangentne vektorje na poljubne črte na površini, tj. lahko se uporablja kot normalni vektor za oblikovanje enačbe tangentne ravnine v točki M 0 (x 0 , l 0 , z 0 ) površine

(4.6)

in kot smerni vektor v normalni enačbi:

(4.7)

V primeru eksplicitne (4.2) dodelitve površine imata enačbi tangentne ravnine oziroma normale obliko:

(4.8)

in
(4.9)

V parametrični predstavitvi površine (4.3) so vektorji
ležijo v tangentni ravnini in enačbo tangentne ravnine lahko zapišemo kot:

(4.10)

in njihov vektorski produkt lahko vzamemo kot usmerjevalni normalni vektor:

in normalno enačbo lahko zapišemo kot:

(4.11)

kje
- vrednosti parametrov, ki ustrezajo točki M 0 .

V nadaljevanju se omejimo na upoštevanje le tistih točk površine, kjer so vektorji

niso enake nič in niso vzporedne.

Primer 4.1 Sestavite enačbi tangentne ravnine in normale v točki M 0 (1,1,2) na površino vrtilnega paraboloida
.

Rešitev: Ker je paraboloidna enačba podana eksplicitno, moramo glede na (4.8) in (4.9) najti
na točki M 0 :

, in v točki M 0
. Nato enačba tangentne ravnine v točki M 0 bo imel obliko:

2(x -1)+2(l -1)-(z-2)=0 ali 2 x +2 l -z - 2=0 in normalna enačba
.

Primer 4.2 Sestavite enačbe tangentne ravnine in normale na poljubni točki na helikoidu
, .

rešitev. tukaj,

Enačba tangentne ravnine:

Normalne enačbe:

4.3 PRVA KVADRATNA OBLIKA POVRŠJA.

Če je površina podana z enačbo

potem krivulja
na njem lahko podamo z enačbo
(4.12)

Diferencial vektorskega radija
vzdolž krivulje, ki ustreza odmiku od točke M 0 do bližnje točke M, je enako

(4.13)

Ker
je diferencial loka krivulje, ki ustreza istemu premiku), potem

(4.14)

kje .

Izraz na desni strani (4.14) se imenuje prva kvadratna oblika površine in ima veliko vlogo v teoriji površin.

Integracijski diferencialds v območju od t 0 (ustreza točki M 0 ) do t (ustreza točki M), dobimo dolžino ustreznega segmenta krivulje

(4.15)

Če poznamo prvo kvadratno obliko površine, lahko najdemo ne samo dolžine, ampak tudi kote med krivuljami.

Če du , dv so razlike krivuljnih koordinat, ki ustrezajo infinitezimalnemu premiku vzdolž ene krivulje, in
— po drugi strani pa ob upoštevanju (4.13):

(4.16)

Uporaba formule

(4.17)

prva kvadratna oblika omogoča izračun površine regije
površine.

Primer 4.3 Na helikoidu poiščite dolžino vijačnice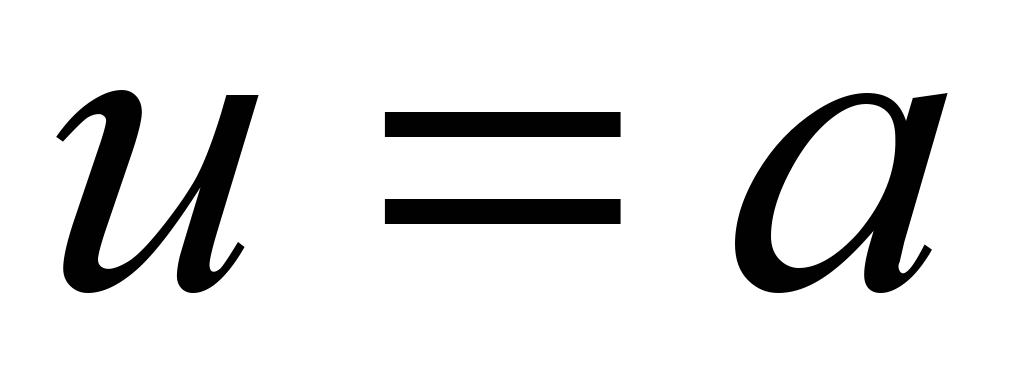
med dvema točkama.

rešitev. Ker na vijačnici
, potem . Poiščite na točki
prva kvadratna oblika. Označuje inv = t , dobimo enačbo te vijačnice v obliki . Kvadratna oblika:

= - prva kvadratna oblika.

Tukaj. V formuli (4.15) v tem primeru
in dolžina loka:

4.4 DRUGA KVADRATNA OBLIKA POVRŠJA.

Označimo
- enotski normalni vektor na površino
:

(4.18) . (4.23)

Črta na površini se imenuje krivulja, če je njena smer v vsaki točki glavna smer.

4.6 POJEM GEODETSKIH ČRT NA POVRŠJU.

Opredelitev 4.1 . Krivulja na površini se imenuje geodetska, če je njena glavna normala na vsaki točki, kjer je ukrivljenost različna od nič, sovpada z normalo na površje.

Skozi vsako točko površja poteka v kateri koli smeri in le ena geodetska. Na krogli so na primer veliki krogi geodetske črte.

Parametracija površine se imenuje polgeodetska, če je ena družina koordinatnih črt sestavljena iz geodetskih črt, druga pa je pravokotna nanjo. Na primer na krogelnih meridianih (geodezijah) in vzporednikih.

Geodezija na dovolj majhnem segmentu je najkrajša med vsemi blizu nje krivuljami, ki povezujejo iste točke.

Enačba normalne ravnine

Tangentna ravnina in normala površine

Naj bo podana neka ploskev, A je fiksna točka ploskve in B je spremenljiva točka ploskve,

(slika 1).

Neničelni vektor

→

klical normalni vektor na površino v točki A, če

lim

B→A

j =

Površinska točka F (x, y, z) = 0 se imenuje navadna, če je na tej točki

parcialni odvodi F " x , F " y , F " z so zvezni;
(F " x )2 + (F " y )2 + (F " z )2 ≠ 0 .

Če je vsaj eden od teh pogojev kršen, se imenuje točka na površini singularna točka površja .

1. izrek.Če je M(x 0 , y 0 , z 0 ) navadna točka ploskve F (x , y , z) = 0 , potem je vektor

→

\u003d grad F (x 0, y 0, z 0) \u003d F "x (x 0, y 0, z 0)

→

jaz

+ F "y (x 0, y 0, z 0)

→

+ F "z (x 0, y 0, z 0)

→

(1)

je normalna na to površino v točki M (x 0 , y 0 , z 0 ) .

Dokaz podan v knjigi I.M. Petrushko, L.A. Kuznecova, V.I. Prohorenko, V.F. Safonova ``Tečaj višje matematike: Integralni račun. Funkcije več spremenljivk. Diferencialne enačbe. M.: Založba MEI, 2002 (str. 128).

Normalno na površino na neki točki se imenuje črta, katere smerni vektor je normalen na površino v tej točki in ki poteka skozi to točko.

Kanonično normalne enačbe lahko predstavljamo kot

x − x0

F "x (x 0, y 0, z 0)

y − y0

F "y (x 0, y 0, z 0)

z − z0

F "z (x 0, y 0, z 0)

(2)

Tangentna ravnina na površino v neki točki se imenuje ravnina, ki poteka skozi to točko pravokotno na normalo na površino v tej točki.

Iz te definicije izhaja, da enačba tangentne ravnine izgleda kot:

(3)

Če je točka na površini singularna, potem na tej točki normalni vektor na površino morda ne obstaja in posledično površina morda nima normalne in tangentne ravnine.

Geometrični pomen totalnega diferenciala funkcije dveh spremenljivk

Naj bo funkcija z = f (x , y) diferenciabilna v točki a (x 0 , y 0 ) . Njegov graf je površina

f (x, y) − z = 0.

Postavimo z 0 = f (x 0 , y 0 ) . Potem točka A (x 0 , y 0 , z 0 ) pripada površini.

Parcialni odvodi funkcije F (x , y , z) = f (x , y) − z so

F " x = f " x , F " y = f " y , F " z = − 1

in v točki A (x 0 , y 0 , z 0 )

so neprekinjeni;
F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0 .

Zato je A navadna točka ploskve F (x, y, z) in v tej točki je tangentna ravnina na ploskev. Glede na (3) ima enačba tangentne ravnine obliko:

f "x (x 0 , y 0 ) (x − x 0 ) + f " y (x 0 , y 0 ) (y − y 0 ) − (z − z 0 ) = 0.

Navpični premik točke na tangentni ravnini pri prehodu iz točke a (x 0 , y 0 ) v poljubno točko p (x , y) je B Q (slika 2). Ustrezen prirast aplikacije je

(z - z 0 ) \u003d f "x (x 0, y 0) (x - x 0) + f" y (x 0, y 0) (y - y 0)

Tukaj na desni strani je diferencial d z funkcije z = f (x, y) v točki a (x 0 , x 0 ). Posledično
d f (x 0, y 0). je prirastek aplikata točke ravnine, ki se dotika grafa funkcije f (x, y) v točki (x 0, y 0, z 0 = f (x 0, y 0 )).

Iz definicije diferenciala sledi, da je razdalja med točko P na grafu funkcije in točko Q na tangentni ravnini infinitezimalno višjega reda kot razdalja od točke p do točke a.

Površina je definirana kot množica točk, katerih koordinate zadoščajo določeni vrsti enačbe:

F (x, y, z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Če funkcija F (x, y, z) (\displaystyle F(x,\,y,\,z)) je na neki točki zvezna in ima na njej zvezne delne odvode, od katerih vsaj ena ne izgine, potem bo v bližini te točke površina, podana z enačbo (1), pravilno površino.

Poleg naštetega impliciten način nastavitve, je mogoče definirati površino jasno, če je eno od spremenljivk, na primer z, mogoče izraziti z drugimi:

z = f (x , y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

Bolj strogo, gladka površina je podoba homeomorfne preslikave (to je ena proti ena in medsebojno zvezne preslikave) notranjosti enotskega kvadrata. Tej definiciji je mogoče dati analitični izraz.

Naj bo na ravnini s pravokotnim koordinatnim sistemom u in v podan kvadrat, katerega koordinate notranjih točk zadovoljujejo neenakosti 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Primer preprosta površina je polkrogla. Celotno območje ni gladka površina. To zahteva nadaljnjo posplošitev koncepta površine.

Podmnožica prostora, v kateri ima vsaka točka sosesko, ki je gladka površina, je poklican pravilno površino .

Površje v diferencialni geometriji

Helikoid

katenoid

Metrika ne določa enolično oblike površine. Na primer, metriki helikoida in katenoida, parametrizirani na ustrezen način, sovpadata, to pomeni, da obstaja ujemanje med njunima regijama, ki ohranja vse dolžine (izometrija). Lastnosti, ki se ohranijo pri izometričnih transformacijah, imenujemo notranja geometrija površine. Notranja geometrija ni odvisna od položaja ploskve v prostoru in se ne spremeni, ko jo upognemo brez napetosti in stiskanja (na primer, ko je valj upognjen v stožec).

Metrični koeficienti E, F, G (\displaystyle E,\ F,\ G) določiti ne samo dolžine vseh krivulj, temveč na splošno rezultate vseh meritev znotraj površine (koti, površine, ukrivljenost itd.). Zato se vse, kar je odvisno samo od metrike, nanaša na notranjo geometrijo.

Običajni in običajni odsek

Normalni vektorji na površinskih točkah

Ena od glavnih značilnosti površine je njena normalno- enotski vektor, pravokoten na tangentno ravnino v dani točki:

m = [r u ′, r v ′] | [r u ′, r v ′] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).

Predznak normale je odvisen od izbire koordinat.

Prerez površja z ravnino, ki vsebuje normalo površja v dani točki, tvori neko krivuljo, ki jo imenujemo običajni oddelek površine. Glavna normala normalnega odseka sovpada z normalo na površino (do znaka).

Če krivulja na površini ni normalni odsek, potem njena glavna normala tvori kot z normalo površine θ (\displaystyle \theta ). Potem ukrivljenost k (\displaystyle k) krivulja je povezana z ukrivljenostjo k n (\displaystyle k_(n)) normalni prerez (z enako tangento) Meunierjeva formula:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Koordinate normalnega vektorja za različne načine podajanja površine so podane v tabeli:

	Normalne koordinate na površini
implicitna dodelitev	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\delni F)(\delni x));\,(\frac (\delni F)(\delni y));\,(\frac (\delni F)(\delni z))\desno) )(\sqrt (\levo((\frac (\delni F)(\delni x))\desno)^(2)+\levo((\frac (\delni F)(\delni y))\desno) ^(2)+\levo((\frac (\delni F)(\delni z))\desno)^(2)))))
eksplicitna dodelitev	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f) )(\delni x));\,-(\frac (\delni f)(\delni y));\,1\desno))(\sqrt (\levo((\frac (\delni f)(\ delno x))\desno)^(2)+\levo((\frac (\delno f)(\delno y))\desno)^(2)+1))))
parametrična naloga	(D (y , z) D (u , v) ; D (z , x) D (u , v) ; D (x , y) D (u , v)) (D (y , z) D (u , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x , y) D (u , v)) 2 (\displaystyle (\frac (\left((\frac (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\desno))(\sqrt (\levo((\frac (D(y,z))(D(u,v)))\desno)^(2 )+\levo((\frac (D(z,x))(D(u,v)))\desno)^(2)+\levo((\frac (D(x,y))(D( u,v)))\desno)^(2)))))

Tukaj D (y , z) D (u , v) = | y u ′ y v ′ z u ′ z v ′ | , D (z , x) D (u , v) = | z u ′ z v ′ x u ′ x v ′ | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

Vse izpeljanke se vzamejo v točki (x 0, y 0, z 0) (\displaystyle (x_(0),y_(0),z_(0))).

Ukrivljenost

Za različne smeri na določeni točki na površini dobimo različno ukrivljenost normalnega odseka, ki se imenuje normalna ukrivljenost; je dodeljen znak plus, če gre glavna normala krivulje v isto smer kot normala na površje, ali znak minus, če sta smeri normale nasprotni.

Na splošno sta na vsaki točki površine dve pravokotni smeri e 1 (\displaystyle e_(1)) in e 2 (\displaystyle e_(2)), pri kateri normalna ukrivljenost zavzame najmanjšo in največjo vrednost; te smeri se imenujejo glavni. Izjema je primer, ko je normalna ukrivljenost enaka v vseh smereh (na primer v bližini krogle ali na koncu vrtilnega elipsoida), potem so vse smeri v točki glavne.

Površine z negativno (levo), ničelno (sredina) in pozitivno (desno) ukrivljenostjo.

Imenujejo se normalne ukrivljenosti v glavnih smereh glavne ukrivljenosti; jih označimo κ 1 (\displaystyle \kappa _(1)) in κ 2 (\displaystyle \kappa _(2)). Velikost:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

Na neki točki in ima na njej zvezne delne odvode, od katerih vsaj ena ne izgine, potem bo v bližini te točke površina, podana z enačbo (1), pravilno površino.

Poleg naštetega impliciten način nastavitve površino je mogoče določiti jasno, če je eno od spremenljivk, na primer z, mogoče izraziti z drugimi:

Prav tako obstaja parametrični metoda dodelitve. V tem primeru je površina določena s sistemom enačb:

Koncept enostavne površine

Natančneje, gladka površina je podoba homeomorfne preslikave (to je ena proti ena in medsebojno zvezne preslikave) notranjosti enotskega kvadrata. Tej definiciji je mogoče dati analitični izraz.

Primer preprosta površina je polkrogla. Celotno območje ni gladka površina. To zahteva nadaljnjo posplošitev koncepta površine.

Podmnožica prostora, v kateri ima vsaka točka sosesko, ki je gladka površina, je poklican pravilno površino .

Površje v diferencialni geometriji

Helikoid

katenoid

Metrični koeficienti ne določajo samo dolžin vseh krivulj, temveč na splošno rezultate vseh meritev znotraj površine (koti, površine, ukrivljenost itd.). Zato se vse, kar je odvisno samo od metrike, nanaša na notranjo geometrijo.

Običajni in običajni odsek

Normalni vektorji na površinskih točkah

Ena od glavnih značilnosti površine je njena normalno- enotski vektor, pravokoten na tangentno ravnino v dani točki:

Predznak normale je odvisen od izbire koordinat.

Presek ploskve z ravnino, ki vsebuje normalo (v dani točki), tvori določeno krivuljo na ploskvi, ki jo imenujemo običajni oddelek površine. Glavna normala normalnega odseka sovpada z normalo na površino (do znaka).

Če krivulja na površini ni normalni odsek, potem njena glavna normala z normalo površine tvori kot θ. Potem ukrivljenost k krivulja je povezana z ukrivljenostjo k n normalni prerez (z enako tangento) Meunierjeva formula:

Koordinate normalnega vektorja za različne načine podajanja površine so podane v tabeli:

	Normalne koordinate na površini
implicitna dodelitev
eksplicitna dodelitev
parametrična naloga

Ukrivljenost

Na splošno sta na vsaki točki površine dve pravokotni smeri e 1 in e 2 , v kateri ima normalna ukrivljenost najmanjšo in največjo vrednost; te smeri se imenujejo glavni. Izjema je primer, ko je normalna ukrivljenost enaka v vseh smereh (na primer v bližini krogle ali na koncu vrtilnega elipsoida), potem so vse smeri v točki glavne.

Površine z negativno (levo), ničelno (sredina) in pozitivno (desno) ukrivljenostjo.

Imenujejo se normalne ukrivljenosti v glavnih smereh glavne ukrivljenosti; označimo jih z κ 1 in κ 2 . Velikost:

K= κ 1 κ 2

klical Gaussova ukrivljenost, polna ukrivljenost ali preprosto ukrivljenost površine. Obstaja tudi izraz skalar ukrivljenosti, ki implicira rezultat konvolucije tenzorja ukrivljenosti ; v tem primeru je skalar ukrivljenosti dvakrat večji od Gaussove ukrivljenosti.

Gaussovo ukrivljenost je mogoče izračunati prek metrike, zato je predmet intrinzične geometrije površin (upoštevajte, da glavne ukrivljenosti ne veljajo za intrinzično geometrijo). Po znaku ukrivljenosti lahko razvrstimo točke površine (glej sliko). Ukrivljenost ravnine je enaka nič. Ukrivljenost krogle s polmerom R je povsod enaka. Obstaja tudi površina stalne negativne ukrivljenosti - psevdosfera.

Geodetske črte, geodetska ukrivljenost

Krivulja na površini se imenuje geodetska linija, ali preprosto geodetski, če v vseh svojih točkah glavna normala na krivuljo sovpada z normalo na površino. Primer: na ravnini bodo geodetske črte ravne črte in segmenti, na krogli - veliki krogi in njihovi segmenti.

Ekvivalentna definicija: za geodetsko črto je projekcija njene glavne normale na sosednjo ravnino ničelni vektor. Če krivulja ni geodetska, je navedena projekcija različna od nič; njena dolžina se imenuje geodetska ukrivljenost k g krivulja na površini. Obstaja razmerje:

kje k je ukrivljenost te krivulje, k n- ukrivljenost njenega normalnega odseka z isto tangento.

Geodetske črte se nanašajo na notranjo geometrijo. Navajamo njihove glavne lastnosti.

Ena in samo ena geodetska črta poteka skozi dano točko na površini v dani smeri.
Na dovolj majhnem območju površine lahko dve točki vedno povežemo z geodezijo, poleg tega pa samo eno. Pojasnilo: na krogli sta nasprotna pola povezana z neskončnim številom meridianov, dve bližnji točki pa lahko povežeta ne le z odsekom velikega kroga, temveč tudi z njegovim dodatkom polnemu krogu, tako da je edinstvenost opažena le v majhnem.
Geodezija je najkrajša. Natančneje: na majhnem koščku površja najkrajša pot med danimi točkami poteka po geodetski črti.

kvadrat

Druga pomembna lastnost površine je njena kvadrat, ki se izračuna po formuli: