Тангентна равнина. Допирателна равнина и повърхност нормални

Тангентните равнини играят голяма роля в геометрията. Изграждането на допирателни равнини в практическо отношение е важно, тъй като тяхното присъствие ви позволява да определите посоката на нормалата към повърхността в точката на контакт. Този проблем се използва широко в инженерната практика. Допирателните равнини се използват и за конструиране на скици на геометрични фигури, ограничени от затворени повърхности. В теоретично отношение равнините, допирателни към повърхност, се използват в диференциалната геометрия за изследване на свойствата на повърхност в областта на допирателна точка.

Основни понятия и дефиниции

Равнината, допирателна към повърхността, трябва да се разглежда като гранично положение на секучната равнина (подобно на линията, допирателна към кривата, която също се дефинира като гранична позиция на секущата).

Равнината, допирателна към повърхността в дадена точка от повърхността, е множеството от всички прави - допирателни, изтеглени към повърхността през дадена точка.

В диференциалната геометрия е доказано, че всички допирателни към повърхност, начертана в обикновена точка, са компланарни (принадлежат на една и съща равнина).

Нека разберем как се начертава права линия, допирателна към повърхността. Допирателната t към повърхността β в точка M, дадена на повърхността (фиг. 203) представлява граничното положение на секущата l j, пресичаща повърхността в две точки (MM 1, MM 2, ..., MM n), когато пресечните точки съвпадат (M ≡ M n , l n ≡ l M). Очевидно (M 1 , M 2 , ..., M n ) ∈ g, тъй като g ⊂ β. Следното определение следва от горното: допирателна към повърхност е линия, допирателна към всяка крива, принадлежаща на повърхността.

Тъй като равнината е дефинирана от две пресичащи се прави линии, за да зададете равнина, допирателна към повърхността в дадена точка, е достатъчно да начертаете две произволни линии, принадлежащи на повърхността (за предпочитане с проста форма) през тази точка, и да построите допирателни към всеки от тях в пресечната точка на тези прави. Конструираните допирателни определят еднозначно допирателната равнина. Визуално представяне на задържането на равнината α, допирателна към повърхността β в дадена точка M, е дадено на фиг. 204. Тази фигура показва и нормалата n към повърхността β.

Нормалката към повърхността в дадена точка е права линия, перпендикулярна на допирателната равнина и минаваща през точката на контакт.

Линията на пресичане на повърхността от равнина, минаваща през нормалата, се нарича нормално сечение на повърхността. В зависимост от вида на повърхността, допирателната равнина може да има с повърхността една или много точки (линия). Линията на контакт може да бъде едновременно и линията на пресичане на повърхността с равнината.

Има и случаи, когато на повърхността има точки, в които е невъзможно да се начертае допирателна към повърхността; такива точки се наричат единични. Като пример за единични точки могат да се дадат точки, принадлежащи на ръба на ръба на торса или точката на пресичане на меридиана на повърхността на въртене с неговата ос, ако меридианът и оста не се пресичат вдясно ъгъл.

Видовете контакт зависят от естеството на кривината на повърхността.

кривина на повърхността

Проблемите с кривината на повърхността са изследвани от френския математик Ф. Дюпен (1784-1873), който предлага визуален начин за изобразяване на промените в кривината на нормалните участъци на повърхността.

За да направите това, в равнина, допирателна към разглежданата повърхност в точка M (фиг. 205, 206), върху допирателни към нормалните сечения от двете страни на тази точка, се начертават сегменти, равни на квадратните корени от стойностите на съответните радиуси на кривина на тези участъци. Множеството от точки - краищата на отсечките определят крива, наречена Индикатриса на Дюпен. Алгоритъмът за конструиране на индикатрисата на Дюпен (фиг. 205) може да се запише:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(R l 1), = √(R l 2),..., = √(R l n)

където R е радиусът на кривината.

(A 1 ∪ A 2 ∪ ... ∪ A n) е индикатрисата на Дюпен.

Ако индикатрисата на Дюпен на повърхността е елипса, тогава точката M се нарича елиптична, а повърхността се нарича повърхност с елипсовидни точки(фиг. 206). В този случай допирателната равнина има само една обща точка с повърхността и всички линии, принадлежащи на повърхността и пресичащи се в разглежданата точка, са разположени от една и съща страна на допирателната равнина. Пример за повърхности с елипсовидни точки са: параболоид на въртене, елипсоид на въртене, сфера (в този случай индикатрисата на Дюпен е кръг и т.н.).

Когато чертаете допирателна равнина към повърхност на торса, равнината ще докосва тази повърхност по права образуваща. Точките от тази права се наричат параболична, а повърхността е повърхност с параболични точки. Индикаторът на Дюпен в този случай е две успоредни прави (фиг. 207*).

На фиг. 208 показва повърхност, състояща се от точки, в които

* Крива от втори ред - парабола - при определени условия може да се разпадне на две реални успоредни прави, две въображаеми успоредни прави, две съвпадащи прави. На фиг. 207 имаме работа с две реални успоредни прави.

Свободна допирателна равнина пресича повърхността. Такава повърхност се нарича хиперболичен, и точките, принадлежащи към него - хиперболични точки. Индикатрисата на Дюпен в този случай е хипербола.

Повърхнина, всички точки на която са хиперболични, има формата на седло (наклонена равнина, еднолистов хиперболоид, вдлъбнати повърхности на въртене и др.).

Една повърхност може да има точки от различен тип, например на повърхността на торса (фиг. 209) точка M е елипсовидна; точка N - параболична; точка K е хиперболична.

В хода на диференциалната геометрия се доказва, че нормалните участъци, в които стойностите на кривината K j = 1/ R j (където R j е радиусът на кривината на разглеждания участък) имат екстремни стойности, са разположени в две взаимно перпендикулярни равнини.

Такива кривини K 1 = 1/R max. K 2 = 1 / R min се наричат основни, а стойностите на H = (K 1 + K 2) / 2 и K = K 1 K 2 - съответно средната кривина на повърхността и общата (гаусова) кривина на повърхността в разглежданата точка. За елиптични точки K > 0, хиперболичен K

Задаване на равнината, допирателна към повърхността на диаграмата на Монж

По-долу, използвайки конкретни примери, ще покажем изграждането на равнина, допирателна към повърхност с елиптични (пример 1), параболични (пример 2) и хиперболични (пример 3) точки.

ПРИМЕР 1. Построете равнина α, допирателна към повърхността на въртене β, с елипсовидни точки. Помислете за два варианта за решаване на този проблем, а) точка M ∈ β и б) точка M ∉ β

Вариант а (фиг. 210).

Допирателната равнина се дефинира от две допирателни t 1 и t 2, начертани в точка M към паралела и меридиана на повърхността β.

Проекциите на допирателната t 1 към паралела h на повърхността β ще бъдат t" 1 ⊥ (S"M") и t" 1 || х ос. Хоризонталната проекция на допирателната t "2 към меридиана d на повърхността β, минаваща през точка M, ще съвпадне с хоризонталната проекция на меридиана. За да се намери фронталната проекция на допирателната t" 2, меридионалната равнина γ (γ ∋ M) чрез завъртане около оста на повърхността β се превежда в позиция γ 1, успоредна на равнината π 2 . В този случай точката M → M 1 (M "1, M" 1) Проекцията на допирателната t "2 rarr; t" 2 1 се определя от (M "1 S"). Ако сега върнем равнината γ 1 в първоначалното й положение, тогава точката S "ще остане на мястото си (като принадлежаща на оста на въртене), а M" 1 → M "и фронталната проекция на допирателната t" 2 ще се определя (M "S")

Две допирателни t 1 и t 2, пресичащи се в точка M ∈ β, определят равнина α, допирателна към повърхността β.

Вариант b (фиг. 211)

За да се построи равнина, допирателна към повърхност, минаваща през точка, която не принадлежи на повърхността, трябва да се изхожда от следните съображения: през точка извън повърхността, състояща се от елипсовидни точки, може да се начертаят много равнини, допирателни към повърхността. Обвивката на тези повърхности ще бъде някаква конична повърхност. Следователно, ако няма допълнителни индикации, тогава проблемът има много решения и в този случай се свежда до начертаване на конична повърхност γ, допирателна към дадената повърхност β.

На фиг. 211 показва конструкцията на конична повърхност γ, допирателна към сферата β. Всяка равнина α, допирателна към коничната повърхност γ, ще бъде допирателна към повърхността β.

За да построим проекции на повърхността γ от точките M "и M" начертаваме допирателни към окръжностите h "и f" - проекциите на сферата. Маркирайте точките на докосване 1 (1" и 1"), 2 (2" и 2"), 3 (3" и 3") и 4 (4" и 4"). Хоризонталната проекция на окръжността - линията на контакт между коничната повърхност и сферата се проектира в [ 1 "2"] За да намерим точките на елипсата, в която тази окръжност е проектирана върху фронталната равнина на проекции, ще използваме паралелите на сферата.

На фиг. 211 по този начин се определят фронталните проекции на точките E и F (E "и F"). Имайки конична повърхност γ, ние построяваме допирателна равнина α към нея. Същност и последователност на графиката

Някои от конструкциите, които трябва да бъдат направени за това, са показани в следващия пример.

ПРИМЕР 2 Построете равнина α, допирателна към повърхност β с параболични точки

Както в пример 1, разгледайте две решения: а) точка N ∈ β; б) точка N ∉ β

Вариант а (ориз 212).

Конична повърхност се отнася до повърхности с параболични точки (виж фиг. 207.) Равнина, допирателна към конична повърхност, я докосва по праволинейна образуваща. За да я построите, трябва:

1) начертайте образуваща SN (S"N" и S"N") през дадена точка N;

2) маркирайте пресечната точка на образуващата (SN) с водача d: (SN) ∩ d = A;

3) начертайте и допирателна t към d в точка А.

Образуващата (SA) и пресичащата я допирателна t определят равнина α, допирателна към коничната повърхност β в дадена точка N*.

Да се начертае равнина α, допирателна към коничната повърхност β и минаваща през точката N, не принадлежи на

* Тъй като повърхността β се състои от параболични точки (с изключение на върха S), допирателната към нея равнина α ще има общо с нея не една точка N, а права линия (SN).

при натискане на дадена повърхност е необходимо:

1) през дадена точка N и връх S на коничната повърхност β начертайте права линия a (a "и a");

2) определете хоризонталната следа на тази линия H a ;

3) начертайте допирателните t "1 и t" 2 на кривата h 0β през H a - хоризонталната следа на коничната повърхност;

4) свържете допирателните точки A (A "и A") и B (B "и B") към горната част на коничната повърхност S (S "и S").

Пресичащи се прави t 1 , (AS) и t 2 , (BS) определят желаните допирателни равнини α 1 и α 2

ПРИМЕР 3. Построете равнина α, допирателна към повърхност β с хиперболични точки.

Точка К (фиг. 214) се намира на повърхността на глобоида (вътрешната повърхност на пръстена).

За да се определи положението на допирателната равнина α, е необходимо:

1) начертайте паралел на повърхността β h(h", h") през точка K;

2) начертайте допирателна през точката K" t" 1 (t" 1 ≡ h");

3) за да се определят посоките на проекциите на допирателната към меридионалното сечение, е необходимо да се начертае равнина γ през точката K и оста на повърхността, хоризонталната проекция t "2 ще съвпада с h 0γ; за да се построи челната проекция на допирателната t" 2, първо превеждаме равнината γ, като я завъртаме около оста на повърхността на въртене до позиция γ 1 || π 2 . В този случай меридионалното сечение от равнината γ ще съвпада с лявата очертателна дъга на фронталната проекция - полукръг g".

Точка K (K", K"), принадлежаща на кривата на меридионалния участък, ще се премести в позиция K 1 (K" 1, K" 1). През K" 1 начертаваме фронтална проекция на допирателната t" 2 1, подравнена с равнината γ 1 || π 2 позиция и маркирайте точката на нейното пресичане с фронталната проекция на оста на въртене S "1. Връщаме равнината γ 1 в първоначалното й положение, точка K" 1 → K "(точка S" 1 ≡ S ") Фронталната проекция на допирателната t" 2 се определя от точки K" и S".

Тангентите t 1 и t 2 определят желаната допирателна равнина α, която пресича повърхността β по кривата l .

ПРИМЕР 4. Построете равнина α, допирателна към повърхността β в точка K. Точката K се намира на повърхността на еднолистов хиперболоид на въртене (фиг. 215).

Този проблем може да бъде решен, като се следва алгоритъма, използван в предишния пример, но като се вземе предвид, че повърхността на еднолистов хиперболоид на въртене е линейка, която има две семейства праволинейни генератори и всеки от генераторите от едно семейство пресича всички генератори от другото семейство (виж § 32, фиг. 138). През всяка точка от тази повърхност могат да се начертаят две пресичащи се прави линии - генератори, които ще бъдат едновременно допирателни към повърхността на еднолистов хиперболоид на въртене.

Тези допирателни определят допирателната равнина, т.е. равнината, допирателна към повърхността на еднолистов хиперболоид на въртене, пресича тази повърхност по две прави линии g 1 и g 2 . За да се построят проекциите на тези прави, е достатъчно да се използва хоризонталната проекция на точка K, за да се пренесат допирателните t "1 и t" 2 към хоризонталата

тала проекция на окръжността d "2 - гърлото на повърхността на еднолистов хиперболоид на въртене; определете точките 1" и 2, в които t "1 и t" 2 пресичат една от повърхностните водачи d 1. От 1" и 2" намираме 1" и 2", които заедно с K" определят челните проекции на желаните линии.

Изтеглете от Depositfiles

4. ТЕОРИЯ НА ПОВЪРХНИТЕ.

4.1 УРАВНЕНИЯ НА ПОВЪРХНОСТИТЕ.

Повърхност в 3D пространство може да бъде дефинирана:

1) имплицитно: Ф ( х , г , z ) =0 (4.1)

2) изрично: z = е ( х , г ) (4.2)

3) параметрично: (4.3)

или:
(4.3’)

къде са скаларните аргументи
понякога се наричат криволинейни координати. Например сфера
удобно е да се задават в сферични координати:
.

4.2 ТАНГЕНТНА РАВНИНА И НОРМАЛНА КЪМ ПОВЪРХНОСТТА.

Ако правата лежи върху повърхността (4.1), тогава координатите на нейните точки удовлетворяват уравнението на повърхността:

Разграничавайки тази идентичност, получаваме:

(4.4)

или
(4.4 ’ )

във всяка точка от кривата на повърхността. По този начин градиентният вектор в неособени точки на повърхността (при които функцията (4.5) е диференцируема и
) е перпендикулярна на допирателните вектори към всякакви линии на повърхността, т.е. може да се използва като нормален вектор за формулиране на уравнението на допирателната равнина в точка M 0 (х 0 , г 0 , z 0 ) повърхности

(4.6)

и като вектор на посоката в нормалното уравнение:

(4.7)

В случай на изрично (4.2) присвояване на повърхността, уравненията на допирателната равнина и на нормата, съответно, приемат вида:

(4.8)

и
(4.9)

В параметричното представяне на повърхността (4.3) векторите
лежат в допирателната равнина и уравнението на допирателната равнина може да се запише като:

(4.10)

и техният векторен продукт може да се приеме като насочващ нормален вектор:

и нормалното уравнение може да се запише като:

(4.11)

където
- стойности на параметрите, съответстващи на точка М 0 .

В това, което следва, ние се ограничаваме до разглеждане само на онези точки от повърхността, където са векторите

не са равни на нула и не са успоредни.

Пример 4.1 Съставете уравненията на допирателната равнина и нормалата в точката M 0 (1,1,2) към повърхността на параболоида на въртене
.

Решение: Тъй като параболоидното уравнение е дадено изрично, съгласно (4.8) и (4.9) трябва да намерим
в точка М 0 :

, а в точката M 0
. Тогава уравнението на допирателната равнина в точката M 0 ще приеме формата:

2(х -1)+2(г -1)-(z-2)=0 или 2 х +2 г -z - 2=0 и нормалното уравнение
.

Пример 4.2 Съставете уравненията на допирателната равнина и нормалата в произволна точка на хеликоида
, .

Решение. Тук ,

Уравнение на допирателната равнина:

или

Нормални уравнения:

4.3 ПЪРВАТА КВАДРАТНА ФОРМА НА ПОВЪРХНОСТТА.

Ако повърхността е дадена от уравнението

след това кривата
върху него може да се даде от уравнението
(4.12)

Радиус векторен диференциал
по кривата, съответстваща на изместването от точка M 0 до близка точка M, е равно на

(4.13)

Като
е диференциалът на дъгата на кривата, съответстваща на същото преместване), тогава

(4.14)

където .

Изразът от дясната страна на (4.14) се нарича първа квадратична форма на повърхността и играе огромна роля в теорията на повърхностите.

Интегриращ диференциалdsвариращи от т 0 (съответства на точка М 0 ) до t (съответства на точка M), получаваме дължината на съответния сегмент от кривата

(4.15)

Познавайки първата квадратна форма на повърхността, можете да намерите не само дължините, но и ъглите между кривите.

Ако ду , dv са диференциалите на криволинейните координати, съответстващи на безкрайно малко изместване по една крива, и
— от друга страна, тогава, като се вземе предвид (4.13):

(4.16)

Използване на формулата

(4.17)

първата квадратна форма дава възможност да се изчисли площта на даден регион
повърхности.

Пример 4.3 На хеликоид намерете дължината на спиралата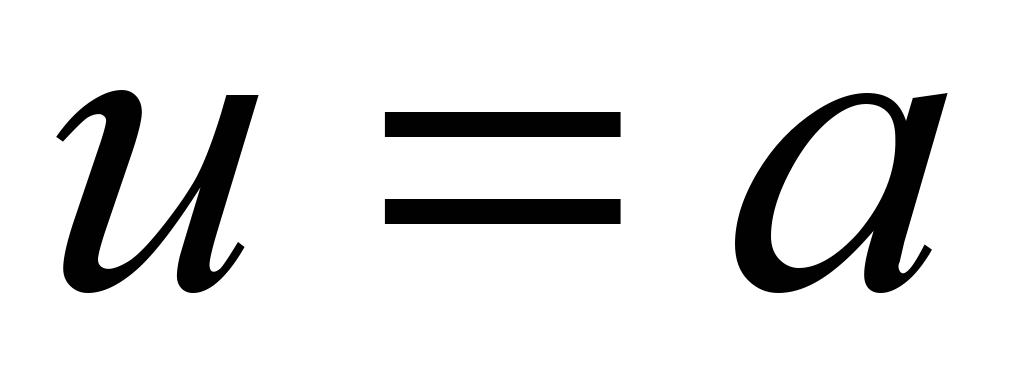
между две точки.

Решение. Защото на спирала
, тогава . Намерете в точка
първата квадратна форма. Обозначавайки иv = т , получаваме уравнението на тази спирала във вида . Квадратна форма:

= - първата квадратна форма.

Тук . Във формула (4.15) в този случай
и дължина на дъгата:

4.4 ВТОРА КВАДРАТНА ФОРМА НА ПОВЪРХНОСТТА.

Означете
- единичен нормален вектор към повърхността
:

(4.18) . (4.23)

Линия върху повърхност се нарича линия на кривина, ако нейната посока във всяка точка е главната посока.

4.6 ПОНЯТИЯТА ЗА ГЕОДЕЗИЧЕСКИ ЛИНИИ ВЪРХУ ПОВЪРХНОСТТА.

Определение 4.1 . Крива върху повърхност се нарича геодезична, ако нейната главна норма е във всяка точка, където кривината е различна от нула, съвпада с нормата на повърхността.

През всяка точка от повърхността във всяка посока минава и само една геодезична. На сфера, например, големите кръгове са геодезични.

Параметризацията на повърхност се нарича полугеодезична, ако едното семейство от координатни линии се състои от геодезични, а другото е ортогонално на нея. Например на сферите меридиани (геодезика) и паралели.

Геодезичната на достатъчно малък сегмент е най-късата сред всички близки до нея криви, свързващи същите точки.

Нормално равнинно уравнение

Допирателна равнина и повърхност нормални

Нека е дадена някаква повърхност, A е фиксирана точка на повърхността и B е променлива точка на повърхността,

(Фиг. 1).

Ненулев вектор

→

Наречен нормален векторна повърхността в точка А, ако

lim

B→A

j =

Повърхностна точка F (x, y, z) = 0 се нарича обикновена, ако е в тази точка

частичните производни F " x , F " y , F " z са непрекъснати;
(F " x )2 + (F " y )2 + (F " z )2 ≠ 0 .

Ако поне едно от тези условия е нарушено, се извиква точка на повърхността единична точка на повърхността .

Теорема 1.Ако M(x 0 , y 0 , z 0 ) е обикновена точка от повърхността F (x , y , z) = 0 , тогава векторът

→

\u003d степен F (x 0, y 0, z 0) \u003d F "x (x 0, y 0, z 0)

→

+ F "y (x 0 , y 0 , z 0 )

→

+ F "z (x 0 , y 0 , z 0 )

→

(1)

е нормален към тази повърхност в точката M (x 0 , y 0 , z 0 ) .

Доказателстводадено в книгата на И.М. Петрушко, Л.А. Кузнецова, V.I. Прохоренко, В.Ф. Сафонова ``Курс по висша математика: Интегрално смятане. Функции на няколко променливи. Диференциални уравнения. М.: Издателство МЕИ, 2002 (стр. 128).

Нормално към повърхносттав дадена точка се нарича права, чийто вектор на посоката е нормален на повърхността в тази точка и която минава през тази точка.

Каноничен нормални уравненияможе да се представи като

x − x0

F "x (x 0, y 0, z 0)

y − y0

F "y (x 0 , y 0 , z 0 )

z−z0

F "z (x 0, y 0, z 0)

(2)

Тангентна равнинакъм повърхността в дадена точка се нарича равнина, която минава през тази точка перпендикулярно на нормалата към повърхността в тази точка.

От това определение следва, че уравнение на допирателната равнинаизглежда като:

(3)

Ако една точка на повърхността е единична, тогава в тази точка векторът, нормален към повърхността, може да не съществува и следователно повърхността може да няма нормална и допирателна равнина.

Геометричното значение на общия диференциал на функция от две променливи

Нека функцията z = f (x, y) е диференцируема в точката a (x 0 , y 0 ) . Неговата графика е повърхността

f (x, y) − z = 0.

Нека поставим z 0 = f (x 0 , y 0 ) . Тогава точката A (x 0 , y 0 , z 0 ) принадлежи на повърхността.

Частичните производни на функцията F (x, y, z) = f (x, y) − z са

F " x = f " x , F " y = f " y , F " z = − 1

и в точка A (x 0 , y 0 , z 0 )

те са непрекъснати;
F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0 .

Следователно A е обикновена точка от повърхността F (x, y, z) и в тази точка има допирателна равнина към повърхността. Съгласно (3) уравнението на допирателната равнина има вида:

f "x (x 0 , y 0 ) (x − x 0 ) + f " y (x 0 , y 0 ) (y − y 0 ) − (z − z 0 ) = 0.

Вертикалното преместване на точка върху допирателната равнина по време на прехода от точка a (x 0 , y 0 ) към произволна точка p (x , y) е B Q (фиг. 2). Съответното увеличение на апликацията е

(z - z 0 ) \u003d f "x (x 0, y 0) (x - x 0) + f" y (x 0, y 0) (y - y 0)

Тук от дясната страна е диференциалът д z на функцията z = f (x, y) в точката a (x 0 , x 0 ). следователно,
д f (x 0 , y 0 ). е нарастването на приложението на точката на равнината, допирателна към графиката на функцията f (x, y) в точката (x 0, y 0, z 0 = f (x 0, y 0 )).

От дефиницията на диференциала следва, че разстоянието между точката P на графиката на функцията и точката Q на допирателната равнина е безкрайно малък по-висок порядък от разстоянието от точка p до точка a.

Повърхността се дефинира като набор от точки, чиито координати удовлетворяват определен тип уравнение:

F (x, y, z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Ако функцията F (x, y, z) (\displaystyle F(x,\,y,\,z))е непрекъсната в някаква точка и има непрекъснати частични производни в нея, поне една от които не изчезва, то в близост до тази точка повърхността, дадена от уравнение (1), ще бъде правилна повърхност.

В допълнение към горното имплицитен начин на настройка, повърхността може да бъде дефинирана ясно, ако една от променливите, например z, може да бъде изразена чрез останалите:

z = f (x, y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

По-строго, обикновена повърхност е образът на хомеоморфно картографиране (тоест едно към едно и взаимно непрекъснато картографиране) на вътрешността на единичния квадрат. На това определение може да се даде аналитичен израз.

Нека е даден квадрат върху равнина с правоъгълна координатна система u и v , координатите на вътрешните точки на която удовлетворяват неравенствата 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Пример проста повърхносте полукълбо. Цялата област не е обикновена повърхност. Това налага допълнително обобщаване на концепцията за повърхност.

Подмножество от пространство, в което всяка точка има съседство, което е обикновена повърхност, е наречен правилна повърхност .

Повърхност в диференциална геометрия

хеликоид

катеноид

Показателят не определя еднозначно формата на повърхността. Например, параметрите на хеликоид и катеноид, параметризирани по подходящ начин, съвпадат, тоест има съответствие между техните региони, което запазва всички дължини (изометрия). Свойствата, които се запазват при изометрични трансформации, се наричат вътрешна геометрияповърхности. Вътрешната геометрия не зависи от положението на повърхността в пространството и не се променя, когато е огъната без опън и компресия (например, когато цилиндърът е огънат в конус).

Метрични коефициенти E , F , G (\displaystyle E,\ F,\ G)определят не само дължините на всички криви, но като цяло резултатите от всички измервания вътре в повърхността (ъгли, площи, кривина и т.н.). Следователно всичко, което зависи само от метриката, се отнася до вътрешната геометрия.

Нормален и нормален раздел

Нормални вектори в точките на повърхността

Една от основните характеристики на повърхността е нейната нормално- единичен вектор, перпендикулярен на допирателната равнина в дадена точка:

m = [ r u ′ , r v ′ ] | [ r u ′ , r v ′ ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).

Знакът на нормата зависи от избора на координати.

Сечението на повърхността от равнина, съдържаща нормалата на повърхността в дадена точка, образува определена крива, която се нарича нормален разделповърхности. Основната норма за нормален участък съвпада с нормалата към повърхността (до знак).

Ако кривата на повърхността не е нормално сечение, тогава нейната главна нормала образува ъгъл с нормалата на повърхността θ (\displaystyle \theta). След това кривината k (\displaystyle k)кривата е свързана с кривината k n (\displaystyle k_(n))нормален участък (със същата допирателна) Формула на Мьоние:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Координатите на нормалния вектор за различни начини за определяне на повърхността са дадени в таблицата:

	Нормални координати в точка на повърхността
имплицитно присвояване	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\left((\frac (\partial F)(\partial z))\right)^(2)))))
изрично задание	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f) )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\ частичен x))\вдясно)^(2)+\вляво((\frac (\partial f)(\partial y))\вдясно)^(2)+1))))
параметрична задача	(D (y, z) D (u, v) ; D (z, x) D (u, v) ; D (x, y) D (u, v)) (D (y, z) D (u , v)) 2 + (D (z, x) D (u, v)) 2 + (D (x, y) D (u, v)) 2 (\displaystyle (\frac (\left((\frac) (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\вдясно))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\вдясно)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\вдясно)^(2)))))

Тук D (y, z) D (u, v) = | y u ′ y v ′ z u ′ z v ′ | , D (z, x) D (u, v) = | z u ′ z v ′ x u ′ x v ′ | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

Всички производни се вземат в точката (x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0))).

Кривина

За различни посоки в дадена точка от повърхността се получава различна кривина на нормалното сечение, което се нарича нормална кривина; приписва му се знак плюс, ако основната нормала на кривата върви в същата посока като нормалата към повърхността, или знак минус, ако посоките на нормалите са противоположни.

Най-общо казано, във всяка точка на повърхността има две перпендикулярни посоки e 1 (\displaystyle e_(1))и e 2 (\displaystyle e_(2)), при което нормалната кривина приема минимални и максимални стойности; тези направления се наричат главен. Изключение е случаят, когато нормалната кривина е една и съща във всички посоки (например близо до сфера или в края на елипсоид на въртене), тогава всички посоки в дадена точка са главни.

Повърхности с отрицателна (ляво), нулева (център) и положителна (дясна) кривина.

Нормалните кривини в главните посоки се наричат главни кривини; нека ги обозначим κ 1 (\displaystyle \kappa _(1))и κ 2 (\displaystyle \kappa _(2)). размер:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

В даден момент и има непрекъснати частични производни в него, поне една от които не изчезва, тогава в близост до тази точка повърхността, дадена от уравнение (1), ще бъде правилна повърхност.

В допълнение към горното имплицитен начин на настройкаповърхността може да се определи ясно, ако една от променливите, например z, може да бъде изразена чрез останалите:

Също така съществува параметриченметод на възлагане. В този случай повърхността се определя от системата от уравнения:

Концепцията за проста повърхност

По-точно, обикновена повърхност е образът на хомеоморфно картографиране (тоест едно към едно и взаимно непрекъснато картографиране) на вътрешността на единичния квадрат. На това определение може да се даде аналитичен израз.

Повърхност в диференциална геометрия

хеликоид

катеноид

Метричните коефициенти определят не само дължините на всички криви, но като цяло резултатите от всички измервания вътре в повърхността (ъгли, площи, кривина и т.н.). Следователно всичко, което зависи само от метриката, се отнася до вътрешната геометрия.

Нормален и нормален раздел

Нормални вектори в точките на повърхността

Знакът на нормата зависи от избора на координати.

Сечението на повърхност от равнина, съдържаща нормалата (в дадена точка), образува определена крива върху повърхността, която се нарича нормален разделповърхности. Основната норма за нормален участък съвпада с нормалата към повърхността (до знак).

Ако кривата на повърхността не е нормално сечение, тогава нейната главна нормала образува ъгъл θ с нормалата на повърхността. След това кривината ккривата е свързана с кривината к ннормален участък (със същата допирателна) Формула на Мьоние:

Координатите на нормалния вектор за различни начини за определяне на повърхността са дадени в таблицата:

	Нормални координати в точка на повърхността
имплицитно присвояване
изрично задание
параметрична задача

Кривина

Най-общо казано, във всяка точка на повърхността има две перпендикулярни посоки д 1 и д 2 , при което нормалната кривина приема минимални и максимални стойности; тези направления се наричат главен. Изключение е случаят, когато нормалната кривина е една и съща във всички посоки (например близо до сфера или в края на елипсоид на въртене), тогава всички посоки в дадена точка са главни.

Повърхности с отрицателна (ляво), нулева (център) и положителна (дясна) кривина.

Нормалните кривини в главните посоки се наричат главни кривини; нека ги означим с κ 1 и κ 2 . размер:

К= κ 1 κ 2

Наречен Гаусова кривина, пълна кривинаили просто кривинаповърхности. Съществува и терминът скаларна кривина, което предполага резултата от навиване на тензора на кривината ; в този случай скаларът на кривината е два пъти по-голям от гаусовата кривина.

Гаусовата кривина може да бъде изчислена от гледна точка на метриката и следователно тя е обект на присъщата геометрия на повърхностите (обърнете внимание, че главните кривини не принадлежат на вътрешната геометрия). По знака на кривина можете да класифицирате точките на повърхността (вижте фигурата). Кривината на равнината е нула. Кривината на сфера с радиус R навсякъде е равна на . Има и повърхност с постоянна отрицателна кривина - псевдосфера.

Геодезически линии, геодезическа кривина

Кривата на повърхността се нарича геодезическа линия, или просто геодезически, ако във всичките си точки основната нормала към кривата съвпада с нормалата към повърхността. Пример: на равнина геодезичните ще бъдат прави линии и отсечки, на сфера - големи кръгове и техните сегменти.

Еквивалентно определение: за геодезическа линия проекцията на нейната главна нормала върху съседната равнина е нулевият вектор. Ако кривата не е геодезична, тогава посочената проекция е различна от нула; дължината му се нарича геодезическа кривина к жкрива на повърхността. Има съотношение:

където ке кривината на тази крива, к н- кривина на нормалното му сечение със същата допирателна.

Геодезичните линии се отнасят до вътрешната геометрия. Изброяваме основните им свойства.

Една и само една геодезична минава през дадена точка на повърхността в дадена посока.
На достатъчно малка площ от повърхността две точки винаги могат да бъдат свързани чрез геодезика и освен това само една. Обяснение: на сфера противоположните полюси са свързани с безкраен брой меридиани и две близки точки могат да бъдат свързани не само чрез сегмент от голям кръг, но и чрез добавянето му към пълен кръг, така че да се наблюдава само уникалност в малка.
Геодезичната е най-кратката. По-строго: на малко парче от повърхността най-краткият път между дадени точки лежи по геодезичната.

Квадрат

Друг важен атрибут на повърхността е нейната квадрат, което се изчислява по формулата: