स्पर्शरेखा विमान। स्पर्शरेखा तल और सतह सामान्य

ज्यामिति में स्पर्शरेखा विमान एक बड़ी भूमिका निभाते हैं। व्यावहारिक रूप से स्पर्शरेखा विमानों का निर्माण महत्वपूर्ण है, क्योंकि उनकी उपस्थिति आपको संपर्क के बिंदु पर सतह पर सामान्य की दिशा निर्धारित करने की अनुमति देती है। इंजीनियरिंग अभ्यास में इस समस्या का व्यापक रूप से उपयोग किया जाता है। बंद सतहों से घिरे ज्यामितीय आकृतियों के रेखाचित्र बनाने के लिए स्पर्शरेखा विमानों का भी उपयोग किया जाता है। सैद्धांतिक शब्दों में, एक सतह के स्पर्शरेखा वाले विमानों को एक स्पर्शरेखा बिंदु के क्षेत्र में सतह के गुणों का अध्ययन करने के लिए अंतर ज्यामिति में उपयोग किया जाता है।

बुनियादी अवधारणाएं और परिभाषाएं

सतह के स्पर्शरेखा वाले समतल को छेदक तल की सीमा स्थिति के रूप में माना जाना चाहिए (वक्र की स्पर्शरेखा के समान, जिसे छेदक की सीमा स्थिति के रूप में भी परिभाषित किया गया है)।

सतह पर किसी दिए गए बिंदु पर सतह पर स्पर्शरेखा समतल सभी रेखाओं का समुच्चय है - किसी दिए गए बिंदु के माध्यम से सतह पर खींची गई स्पर्शरेखाएँ।

विभेदक ज्यामिति में, यह साबित होता है कि एक साधारण बिंदु पर खींची गई सतह पर सभी स्पर्शरेखा समतल होती हैं (एक ही तल की होती हैं)।

आइए जानें कि सतह पर एक सीधी रेखा कैसे खींची जाती है। सतह पर दिए गए बिंदु M पर सतह पर स्पर्शरेखा t (चित्र। 203) सतह को दो बिंदुओं (MM 1, MM 2, ..., MM n) पर प्रतिच्छेद करने वाले छेदक l j की सीमित स्थिति को दर्शाता है, जब चौराहे के बिंदु मेल खाते हैं (एम ≡ एम एन , एल एन ≡ एल एम)। स्पष्ट रूप से (एम 1, एम 2, ..., एम एन) जी, चूंकि जी β। निम्नलिखित परिभाषा ऊपर से निम्नानुसार है: एक सतह के लिए एक स्पर्शरेखा सतह से संबंधित किसी भी वक्र के लिए एक स्पर्श रेखा है.

चूँकि समतल को दो प्रतिच्छेदी सीधी रेखाओं द्वारा परिभाषित किया जाता है, किसी दिए गए बिंदु पर सतह पर एक समतल स्पर्शरेखा सेट करने के लिए, यह इस बिंदु के माध्यम से सतह से संबंधित दो मनमानी रेखाएँ (अधिमानतः सरल आकार में) खींचने के लिए पर्याप्त है, और स्पर्शरेखा का निर्माण करने के लिए पर्याप्त है उनमें से प्रत्येक इन रेखाओं के प्रतिच्छेदन बिंदु पर . निर्मित स्पर्शरेखा विशिष्ट रूप से स्पर्शरेखा तल का निर्धारण करती हैं। किसी दिए गए बिंदु M पर सतह β की स्पर्शरेखा, समतल α के धारण का एक दृश्य निरूपण चित्र में दिया गया है। 204. यह आंकड़ा सतह β के सामान्य n को भी दर्शाता है।

किसी दिए गए बिंदु पर सतह के लिए सामान्य स्पर्शरेखा विमान के लंबवत और संपर्क बिंदु से गुजरने वाली एक सीधी रेखा है।

अभिलंब से गुजरने वाले समतल द्वारा सतह के प्रतिच्छेदन की रेखा को सतह का सामान्य खंड कहा जाता है। सतह के प्रकार के आधार पर, स्पर्शरेखा तल में, सतह के साथ, एक या कई बिंदु (रेखा) हो सकते हैं। संपर्क की रेखा एक ही समय में विमान के साथ सतह के चौराहे की रेखा हो सकती है।

ऐसे मामले भी होते हैं जब सतह पर ऐसे बिंदु होते हैं जहां सतह पर स्पर्शरेखा खींचना असंभव होता है; ऐसे बिंदुओं को एकवचन कहा जाता है। एकवचन बिंदुओं के एक उदाहरण के रूप में, कोई धड़ की सतह के पुच्छ किनारे से संबंधित बिंदु दे सकता है, या अपनी धुरी के साथ क्रांति की सतह के मेरिडियन के चौराहे के बिंदु को दे सकता है, अगर मेरिडियन और अक्ष एक सही पर एक दूसरे को नहीं काटते हैं कोण।

संपर्क के प्रकार सतह की वक्रता की प्रकृति पर निर्भर करते हैं।

सतह वक्रता

सतह की वक्रता के मुद्दों की जांच फ्रांसीसी गणितज्ञ एफ। डुपिन (1784-1873) ने की, जिन्होंने सतह के सामान्य वर्गों की वक्रता में परिवर्तन को दर्शाने का एक दृश्य तरीका प्रस्तावित किया।

ऐसा करने के लिए, बिंदु एम (छवि 205, 206) पर विचाराधीन सतह के स्पर्शरेखा में, इस बिंदु के दोनों किनारों पर सामान्य वर्गों के स्पर्शरेखा पर, खंडों को मानों के वर्गमूल के बराबर प्लॉट किया जाता है इन वर्गों की वक्रता की संगत त्रिज्या। बिंदुओं का समुच्चय - खंडों के सिरे एक वक्र को परिभाषित करते हैं जिसे कहा जाता है डुपिन का संकेतक. डुपिन संकेतक (चित्र 205) के निर्माण के लिए एल्गोरिदम लिखा जा सकता है:

1. एम α, एम β ∧ α β;

2. = (आर एल 1), = √(आर एल 2),..., = (आर एल एन)

जहाँ R वक्रता त्रिज्या है।

(ए 1 ∪ ए 2 ∪ ... ∪ ए एन) डुपिन संकेतक है।

यदि किसी सतह का डुपिन संकेतक एक दीर्घवृत्त है, तो बिंदु M को अण्डाकार कहा जाता है, और सतह को अण्डाकार बिंदुओं वाला पृष्ठ कहा जाता है।(चित्र। 206)। इस मामले में, स्पर्शरेखा तल में सतह के साथ केवल एक सामान्य बिंदु होता है, और सतह से संबंधित सभी रेखाएं और विचाराधीन बिंदु पर प्रतिच्छेद करने वाली सभी रेखाएं स्पर्शरेखा तल के एक ही तरफ स्थित होती हैं। अण्डाकार बिंदुओं के साथ सतहों का एक उदाहरण है: क्रांति का एक परवलयिक, क्रांति का एक दीर्घवृत्त, एक गोला (इस मामले में, डुपिन संकेतक एक चक्र है, आदि)।

धड़ की सतह पर स्पर्शरेखा विमान खींचते समय, विमान इस सतह को एक सीधे जेनरेटर के साथ स्पर्श करेगा। इस रेखा के बिंदु कहलाते हैं परवलयिक, और सतह परवलयिक बिंदुओं वाली एक सतह है. इस मामले में डुपिन संकेतक दो समानांतर रेखाएं हैं (चित्र 207*)।

अंजीर पर। 208 बिंदुओं से युक्त एक सतह को दर्शाता है जिसमें

* दूसरे क्रम का एक वक्र - एक परवलय - कुछ शर्तों के तहत दो वास्तविक समानांतर रेखाओं, दो काल्पनिक समानांतर रेखाओं, दो संयोग रेखाओं में टूट सकता है। अंजीर पर। 207 हम दो वास्तविक समानांतर रेखाओं के बारे में बात कर रहे हैं।

एक ढीला स्पर्शरेखा विमान सतह को काटता है। ऐसी सतह को कहा जाता है अतिपरवलिक, और उससे संबंधित बिंदु - अतिशयोक्तिपूर्ण अंक। इस मामले में ड्यूपिन का संकेतक अतिशयोक्ति है।

एक सतह, जिसके सभी बिंदु अतिशयोक्तिपूर्ण हैं, में एक काठी (तिरछा विमान, एक-शीट वाला हाइपरबोलाइड, क्रांति की अवतल सतह, आदि) का रूप होता है।

एक सतह में विभिन्न प्रकार के बिंदु हो सकते हैं, उदाहरण के लिए, धड़ की सतह पर (चित्र। 209) बिंदु M अण्डाकार है; बिंदु एन - परवलयिक; बिंदु K अतिपरवलयिक है।

विभेदक ज्यामिति के दौरान, यह साबित होता है कि सामान्य खंड, जिसमें वक्रता मान K j = 1/ R j (जहाँ R j माने गए खंड की वक्रता की त्रिज्या है) के चरम मान हैं, दो में स्थित हैं परस्पर लंबवत विमान।

इस तरह की वक्रता K 1 = 1/R अधिकतम। K 2 \u003d 1 / R मिनट को मुख्य कहा जाता है, और H \u003d (K 1 + K 2) / 2 और K \u003d K 1 K 2 के मान क्रमशः, औसत वक्रता विचाराधीन बिंदु पर सतह की सतह और कुल (गाऊसी) वक्रता। अण्डाकार बिंदुओं के लिए K > 0, अतिपरवलयिक K

मोंगे आरेख पर समतल स्पर्शरेखा को सतह पर सेट करना

नीचे, विशिष्ट उदाहरणों का उपयोग करते हुए, हम अण्डाकार (उदाहरण 1), परवलयिक (उदाहरण 2) और अतिपरवलयिक (उदाहरण 3) बिंदुओं के साथ एक सतह पर स्पर्शरेखा के निर्माण को दिखाएंगे।

उदाहरण 1. एक समतल α की रचना कीजिए, जो β क्रांति की सतह पर अण्डाकार बिंदुओं के साथ स्पर्शरेखा हो। इस समस्या को हल करने के लिए दो विकल्पों पर विचार करें, a) एक बिंदु M β और b) एक बिंदु M β

विकल्प ए (चित्र। 210)।

स्पर्शरेखा तल को दो स्पर्शरेखा t 1 और t 2 द्वारा परिभाषित किया गया है जो बिंदु M पर सतह β के समानांतर और मध्याह्न रेखा पर खींची गई है।

सतह β के समानांतर h पर स्पर्शरेखा t 1 का अनुमान t" 1 (S"M") और t" 1 || होगा। एक्स अक्ष। सतह β के मेरिडियन डी के लिए स्पर्शरेखा टी "2 का क्षैतिज प्रक्षेपण, बिंदु एम के माध्यम से गुजर रहा है, मेरिडियन के क्षैतिज प्रक्षेपण के साथ मेल खाएगा। टेंगेंट टी" 2 के ललाट प्रक्षेपण को खोजने के लिए, मेरिडियन विमान γ (γ M) सतह के अक्ष के चारों ओर घुमाकर β को विमान π 2 के समानांतर स्थिति γ 1 में अनुवादित किया जाता है। इस स्थिति में, बिंदु M → M 1 (M "1, M" 1)। स्पर्शरेखा t "2 rarr; t" 2 1 का प्रक्षेपण (M "1 S") द्वारा निर्धारित किया जाता है। यदि हम अब विमान γ 1 को उसकी मूल स्थिति में लौटाते हैं, तो बिंदु S "स्थान पर बना रहेगा (घूर्णन की धुरी से संबंधित), और M" 1 → M "और स्पर्शरेखा t" 2 का ललाट प्रक्षेपण होगा निर्धारित किया जाना (एम "एस")

एक बिंदु M ∈ β पर प्रतिच्छेद करते हुए दो स्पर्शरेखा t 1 और t 2 सतह β पर एक समतल α स्पर्शरेखा को परिभाषित करते हैं।

विकल्प बी (चित्र 211)

एक ऐसे बिंदु से गुजरने वाली सतह पर एक समतल स्पर्शरेखा का निर्माण करने के लिए, जो सतह से संबंधित नहीं है, किसी को निम्नलिखित विचारों से आगे बढ़ना चाहिए: सतह के बाहर एक बिंदु के माध्यम से अण्डाकार बिंदुओं से मिलकर, कोई सतह पर स्पर्शरेखा वाले कई विमानों को खींच सकता है। इन सतहों का लिफाफा कुछ शंक्वाकार सतह होगा। इसलिए, यदि कोई अतिरिक्त संकेत नहीं हैं, तो समस्या के कई समाधान हैं और इस मामले में एक शंक्वाकार सतह खींचने के लिए कम हो जाता है दी गई सतह पर स्पर्शरेखा β।

अंजीर पर। 211 एक शंक्वाकार सतह के निर्माण को दर्शाता है गोले के स्पर्शरेखा β। शंक्वाकार सतह γ के लिए कोई भी विमान α स्पर्शरेखा सतह β के स्पर्शरेखा होगा।

सतह के अनुमानों का निर्माण करने के लिए बिंदु M "और M" से हम वृत्तों पर स्पर्शरेखा खींचते हैं h "और f" - गोले के अनुमान। स्पर्श बिंदु 1 (1 "और 1"), 2 (2" और 2 "), 3 (3" और 3 ") और 4 (4" और 4 ") चिह्नित करें। वृत्त का क्षैतिज प्रक्षेपण - शंक्वाकार सतह और गोले के बीच संपर्क की रेखा को [ 1 "2"] में प्रक्षेपित किया जाता है। गोले के समानांतर।

अंजीर पर। 211 इस तरह, अंक ई और एफ (ई "और एफ") के ललाट अनुमानों को निर्धारित किया जाता है। एक शंक्वाकार सतह γ होने पर, हम इसके लिए एक स्पर्शरेखा विमान α बनाते हैं। ग्राफिक की प्रकृति और अनुक्रम

इसके लिए जिन कुछ निर्माणों को करने की आवश्यकता है, उन्हें निम्नलिखित उदाहरण में दिखाया गया है।

उदाहरण 2 परवलयिक बिंदुओं के साथ एक सतह β स्पर्शरेखा के लिए एक समतल α की रचना करें

जैसा कि उदाहरण 1 में है, दो हलों पर विचार कीजिए। क) बिंदु N β; बी) बिंदु एन β

विकल्प ए (चावल 212)।

एक शंक्वाकार सतह परवलयिक बिंदुओं के साथ सतहों को संदर्भित करती है (चित्र 207 देखें।) एक शंक्वाकार सतह के लिए एक स्पर्शरेखा इसे एक रेक्टिलिनियर जेनरेट्रिक्स के साथ स्पर्श करती है। इसे बनाने के लिए, आपको यह करना होगा:

1) दिए गए बिंदु N से होकर एक जेनरेटर SN (S"N" और S"N") खींचिए;

2) गाइड डी के साथ जेनरेटरिक्स (एसएन) के चौराहे बिंदु को चिह्नित करें: (एसएन) डी = ए;

3) बिंदु A पर t से d तक खींचे और स्पर्श करें।

जेनरेट्रिक्स (एसए) और टेंगेंट टी इसे प्रतिच्छेद करते हैं, एक विमान α स्पर्शरेखा को शंक्वाकार सतह β पर दिए गए बिंदु N* पर परिभाषित करते हैं।

शंक्वाकार सतह β पर एक समतल α स्पर्शरेखा खींचने के लिए और बिंदु N से गुजरने का संबंध नहीं है

* चूंकि सतह β में परवलयिक बिंदु होते हैं (शीर्ष S को छोड़कर), विमान α इसके साथ स्पर्शरेखा में एक बिंदु N नहीं, बल्कि एक सीधी रेखा (SN) होगी।

किसी दिए गए सतह को दबाकर, यह आवश्यक है:

1) दिए गए बिंदु N और शंक्वाकार सतह के एक शीर्ष S से होकर एक सीधी रेखा a (a "और a") खींचे;

2) इस रेखा H a का क्षैतिज अनुरेखण ज्ञात कीजिए;

3) वक्र h 0β से H a के स्पर्शरेखा t "1 और t" 2 खींचें - शंक्वाकार सतह का क्षैतिज निशान;

4) स्पर्शरेखा बिंदु A (A "और A") और B (B "और B") को शंक्वाकार सतह S (S "और S") के शीर्ष से कनेक्ट करें।

प्रतिच्छेदी रेखाएँ t 1, (AS) और t 2 , (BS) वांछित स्पर्शरेखा समतल α 1 और α 2 को परिभाषित करती हैं

उदाहरण 3. अतिपरवलयिक बिंदुओं के साथ सतह β पर एक समतल α स्पर्शरेखा की रचना कीजिए।

बिंदु K (चित्र 214) ग्लोबिड (अंगूठी की आंतरिक सतह) की सतह पर स्थित है।

स्पर्शरेखा विमान α की स्थिति निर्धारित करने के लिए, यह आवश्यक है:

1) बिंदु K से होकर सतह β h(h", h") के समानांतर एक रेखा खींचिए;

2) बिंदु K" t" 1 (t" 1 h") के माध्यम से एक स्पर्शरेखा बनाएं;

3) मध्याह्न खंड के स्पर्शरेखा के अनुमानों की दिशाओं को निर्धारित करने के लिए, बिंदु K और सतह के अक्ष के माध्यम से एक विमान खींचना आवश्यक है, क्षैतिज प्रक्षेपण t "2 h 0γ के साथ मेल खाएगा; निर्माण करने के लिए स्पर्शरेखा t" 2 के ललाट प्रक्षेपण के लिए, हम पहले समतल γ को क्रांति की सतह के अक्ष के चारों ओर घुमाकर स्थिति γ 1 || में घुमाते हैं। 2। इस मामले में, विमान द्वारा मध्याह्न खंड ललाट प्रक्षेपण के बाएं रूपरेखा चाप के साथ मेल खाएगा - अर्धवृत्त जी"।

बिंदु K (K", K"), जो मध्याह्न खंड के वक्र से संबंधित है, K 1 (K" 1, K" 1) की स्थिति में चला जाएगा। K" 1 के माध्यम से हम समतल γ 1 || . के साथ संरेखित स्पर्शरेखा t" 2 1 का ललाट प्रक्षेपण बनाते हैं π 2 स्थिति और इसके चौराहे के बिंदु को रोटेशन S "1 के ललाट प्रक्षेपण के साथ चिह्नित करें। हम विमान γ 1 को उसकी मूल स्थिति में लौटाते हैं, बिंदु K" 1 → K "(बिंदु S" 1 ≡ S ") . स्पर्शरेखा t" 2 का ललाट प्रक्षेपण बिंदु K" और S" द्वारा निर्धारित किया जाता है।

स्पर्शरेखा t 1 और t 2 वांछित स्पर्शरेखा समतल α को परिभाषित करते हैं, जो सतह β को वक्र l के अनुदिश काटती है।

उदाहरण 4. एक समतल α स्पर्शरेखा की रचना कीजिए जो सतह β पर बिंदु K पर है। बिंदु K, क्रांति के एक-शीट वाले अतिपरवलयज (चित्र 215) की सतह पर स्थित है।

पिछले उदाहरण में उपयोग किए गए एल्गोरिदम का पालन करके इस समस्या को हल किया जा सकता है, लेकिन यह ध्यान में रखते हुए कि क्रांति के एक-शीट वाले हाइपरबोलाइड की सतह एक शासित सतह है जिसमें रेक्टिलिनियर जनरेटर के दो परिवार होते हैं, और एक परिवार के प्रत्येक जनरेटर दूसरे परिवार के सभी जनित्रों को प्रतिच्छेद करता है (देखें 32, चित्र 138)। इस सतह के प्रत्येक बिंदु के माध्यम से, दो प्रतिच्छेदी सीधी रेखाएँ खींची जा सकती हैं - जनरेटर जो एक साथ क्रांति के एक-शीट वाले हाइपरबोलाइड की सतह पर स्पर्शरेखा होंगे।

ये स्पर्श रेखाएं स्पर्शरेखा तल को परिभाषित करती हैं, अर्थात क्रांति के एक-शीट वाले अतिपरवलयज की सतह पर स्पर्श रेखा इस सतह को दो सीधी रेखाओं g 1 और g 2 के साथ प्रतिच्छेद करती है। इन रेखाओं के अनुमानों का निर्माण करने के लिए, बिंदु K के क्षैतिज प्रक्षेपण का उपयोग करने के लिए स्पर्शरेखा t "1 और t" 2 को क्षैतिज तक ले जाना पर्याप्त है।

सर्कल का थाल प्रोजेक्शन d "2 - क्रांति के सिंगल-शीटेड हाइपरबोलाइड की सतह का गला; उन बिंदुओं को निर्धारित करें 1" और 2 जिस पर t "1 और t" 2 सतह गाइडों में से एक को काटते हैं d 1. 1" और 2" से हम 1" और 2" पाते हैं, जो K के साथ मिलकर वांछित रेखाओं के ललाट अनुमानों को निर्धारित करते हैं।

डिपॉजिटफाइल्स से डाउनलोड करें

4. सतहों का सिद्धांत।

4.1 सतहों के समीकरण।

3D अंतरिक्ष में एक सतह को परिभाषित किया जा सकता है:

1) परोक्ष रूप से: एफ ( एक्स , आप , जेड ) =0 (4.1)

2) स्पष्ट रूप से: जेड = एफ ( एक्स , आप ) (4.2)

3) पैरामीट्रिक रूप से: (4.3)

या:
(4.3’)

अदिश तर्क कहाँ हैं
कभी-कभी वक्रीय निर्देशांक कहा जाता है। उदाहरण के लिए, एक गोला
गोलाकार निर्देशांक में सेट करना सुविधाजनक है:
.

4.2 स्पर्शरेखा समतल और सतह पर सामान्य।

यदि रेखा पृष्ठ (4.1) पर स्थित है, तो इसके बिंदुओं के निर्देशांक पृष्ठीय समीकरण को संतुष्ट करते हैं:

इस पहचान को अलग करते हुए, हम प्राप्त करते हैं:

(4.4)

या
(4.4 ’ )

सतह पर वक्र के प्रत्येक बिंदु पर। इस प्रकार, सतह के गैर-एकवचन बिंदुओं पर ढाल वेक्टर (जिस पर फ़ंक्शन (4.5) भिन्न होता है और
) सतह पर किसी भी रेखा के स्पर्शरेखा वैक्टर के लंबवत है, यानी बिंदु एम पर टेंगेंट विमान के समीकरण को तैयार करने के लिए सामान्य वेक्टर के रूप में उपयोग किया जा सकता है 0 (एक्स 0 , आप 0 , जेड 0 ) सतह

(4.6)

और सामान्य समीकरण में एक दिशा वेक्टर के रूप में:

(4.7)

सतह के एक स्पष्ट (4.2) असाइनमेंट के मामले में, स्पर्शरेखा विमान और सामान्य के समीकरण क्रमशः, रूप लेते हैं:

(4.8)

और
(4.9)

सतह (4.3) के पैरामीट्रिक प्रतिनिधित्व में, वैक्टर
स्पर्शरेखा तल में स्थित है और स्पर्शरेखा तल के समीकरण को इस प्रकार लिखा जा सकता है:

(4.10)

और उनके वेक्टर उत्पाद को सामान्य वेक्टर के निर्देशन के रूप में लिया जा सकता है:

और सामान्य समीकरण को इस प्रकार लिखा जा सकता है:

(4.11)

कहाँ पे
- बिंदु M . के अनुरूप पैरामीटर मान 0 .

इस प्रकार, हम स्वयं को केवल सतह के उन बिंदुओं पर विचार करने तक सीमित रखते हैं जहां वैक्टर

शून्य के बराबर नहीं हैं और समानांतर नहीं हैं।

उदाहरण 4.1 बिंदु M . पर स्पर्शरेखा तल और अभिलंब के समीकरण लिखिए 0 (1,1,2) क्रांति के परवलयिक की सतह पर
.

हल: चूँकि परवलयिक समीकरण स्पष्ट रूप से दिया गया है, (4.8) और (4.9) के अनुसार हमें ज्ञात करना होगा
बिंदु M . पर 0 :

, और बिंदु M 0 . पर
. तब बिंदु M . पर स्पर्शरेखा तल का समीकरण 0 फॉर्म लेगा:

2(एक्स -1)+2(आप -1)-(जेड-2) = 0 या 2 एक्स +2 आप -ज़ू - 2=0, और सामान्य समीकरण
.

उदाहरण 4.2 हेलिकॉइड पर एक मनमाना बिंदु पर स्पर्शरेखा विमान और सामान्य के समीकरणों की रचना करें
, .

फेसला। यहां ,

स्पर्शरेखा समतल समीकरण:

या

सामान्य समीकरण:

4.3 सतह का पहला द्विघात रूप।

यदि सतह समीकरण द्वारा दी गई है

फिर वक्र
उस पर समीकरण द्वारा दिया जा सकता है
(4.12)

त्रिज्या वेक्टर अंतर
बिंदु M . से विस्थापन के संगत वक्र के अनुदिश 0 पास के बिंदु M के बराबर है

(4.13)

जैसा
समान विस्थापन के संगत वक्र चाप का अंतर है), तो

(4.14)

कहाँ पे ।

(4.14) के दायीं ओर के व्यंजक को पृष्ठ का प्रथम द्विघात रूप कहा जाता है और यह सतहों के सिद्धांत में बहुत बड़ी भूमिका निभाता है।

अंतर को एकीकृत करनाडी एससे लेकर टी 0 (बिंदु M . से मेल खाती है) 0) से टी (बिंदु एम के अनुरूप), हम वक्र के संबंधित खंड की लंबाई प्राप्त करते हैं

(4.15)

सतह के पहले द्विघात रूप को जानने के बाद, आप न केवल लंबाई, बल्कि वक्रों के बीच के कोणों का भी पता लगा सकते हैं।

यदि एक ड्यू , डीवी एक वक्र के साथ एक अन्तर्निहित विस्थापन के अनुरूप वक्रीय निर्देशांक के अंतर हैं, और
- दूसरी ओर, ध्यान में रखते हुए (4.13):

(4.16)

सूत्र का उपयोग करना

(4.17)

पहला द्विघात रूप किसी क्षेत्र के क्षेत्रफल की गणना करना संभव बनाता है
सतहें।

उदाहरण 4.3 एक हेलिकॉइड पर, हेलिक्स की लंबाई ज्ञात कीजिए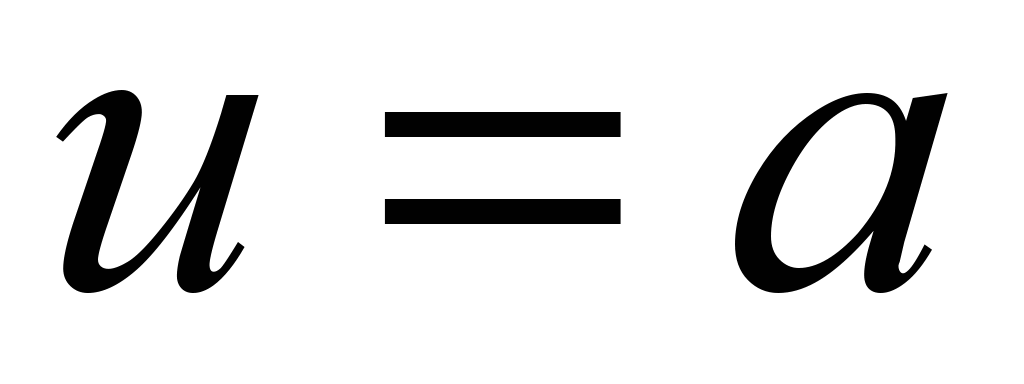
दो बिंदुओं के बीच।

फेसला। क्योंकि एक हेलिक्स पर
, तब । एक बिंदु पर खोजें
पहला द्विघात रूप। नकारना औरवी = टी , हम इस हेलिक्स के समीकरण को रूप में प्राप्त करते हैं। द्विघात आकार:

= - पहला द्विघात रूप।

यहां । इस मामले में सूत्र (4.15) में
और चाप लंबाई:

4.4 सतह का दूसरा द्विघात रूप।

निरूपित
- सतह पर इकाई सामान्य वेक्टर
:

(4.18) . (4.23)

सतह पर एक रेखा वक्रता रेखा कहलाती है यदि प्रत्येक बिंदु पर इसकी दिशा मुख्य दिशा हो।

4.6 सतह पर भूगर्भीय रेखाओं की अवधारणा।

परिभाषा 4.1 . एक सतह पर एक वक्र को जियोडेसिक कहा जाता है यदि इसका प्रमुख सामान्य है हर बिंदु पर जहां वक्रता शून्य नहीं है, सामान्य के साथ मेल खाता है ज़मीनी स्तर पर।

सतह के प्रत्येक बिंदु से किसी भी दिशा में गुजरता है, और केवल एक जियोडेसिक होता है। एक गोले पर, उदाहरण के लिए, बड़े वृत्त जियोडेसिक्स होते हैं।

एक सतह के पैरामीट्रिजेशन को सेमी-जियोडेसिक कहा जाता है यदि समन्वय रेखाओं के एक परिवार में जियोडेसिक्स होते हैं और दूसरा इसके लिए ऑर्थोगोनल होता है। उदाहरण के लिए, गोले पर मेरिडियन (जियोडेसिक्स) और समानताएं।

पर्याप्त रूप से छोटे खंड पर एक जियोडेसिक समान बिंदुओं को जोड़ने वाले सभी वक्रों में सबसे छोटा होता है।

सामान्य समतल समीकरण

स्पर्शरेखा तल और सतह सामान्य

मान लीजिए कि कुछ सतह दी गई है, A सतह का एक निश्चित बिंदु है और B सतह का एक चर बिंदु है,

(चित्र .1)।

गैर-शून्य वेक्टर

→

एन

बुलाया सामान्य वेक्टरबिंदु A पर सतह पर यदि

लिम

बी → ए

जे =

एक सतह बिंदु F (x, y, z) = 0 को सामान्य कहा जाता है यदि इस बिंदु पर

आंशिक व्युत्पन्न F " x , F " y , F " z निरंतर हैं;
(एफ "एक्स)2 + (एफ" वाई)2 + (एफ" जेड)2 0।

यदि इनमें से कम से कम एक शर्त का उल्लंघन किया जाता है, तो सतह पर एक बिंदु कहलाता है सतह का एकवचन बिंदु .

प्रमेय 1.अगर एम (एक्स 0 , y 0 , z 0) सतह F (x , y , z) = 0 का एक सामान्य बिंदु है, तो सदिश

→

एन

\u003d ग्रेड एफ (एक्स 0, वाई 0, जेड 0) \u003d एफ "एक्स (एक्स 0, वाई 0, जेड 0)

→

मैं

+ एफ "वाई (एक्स 0, वाई 0, जेड 0)

→

जे

+ एफ "जेड (एक्स 0, वाई 0, जेड 0)

→

क

(1)

बिंदु M (x 0 , y 0 , z 0) पर इस सतह के लिए सामान्य है।

प्रमाणआई.एम. द्वारा पुस्तक में दिया गया है। पेट्रुस्को, एल.ए. कुज़नेत्सोवा, वी.आई. प्रोखोरेंको, वी.एफ. सफोनोवा `` उच्च गणित का पाठ्यक्रम: इंटीग्रल कैलकुलस। कई चर के कार्य। विभेदक समीकरण। एम.: एमईआई पब्लिशिंग हाउस, 2002 (पृष्ठ 128)।

सतह के लिए सामान्यकिसी बिंदु पर एक रेखा कहलाती है जिसका दिशा वेक्टर इस बिंदु पर सतह के लिए सामान्य है और जो इस बिंदु से गुजरती है।

कैनन का सामान्य समीकरणके रूप में प्रतिनिधित्व किया जा सकता है

एक्स - एक्स0

एफ "एक्स (एक्स 0, वाई 0, जेड 0)

y - y0

एफ "वाई (एक्स 0, वाई 0, जेड 0)

z−z0

एफ "जेड (एक्स 0, वाई 0, जेड 0)

(2)

स्पर्शरेखा विमानकिसी बिंदु पर सतह के लिए एक विमान कहा जाता है जो इस बिंदु से उस बिंदु पर सतह पर सामान्य से लंबवत गुजरता है।

इस परिभाषा से यह इस प्रकार है कि स्पर्शरेखा समतल समीकरणकी तरह लगता है:

(3)

यदि सतह पर एक बिंदु एकवचन है, तो इस बिंदु पर सतह पर सामान्य वेक्टर मौजूद नहीं हो सकता है, और इसके परिणामस्वरूप, सतह में एक सामान्य और स्पर्शरेखा विमान नहीं हो सकता है।

दो चर के एक समारोह के कुल अंतर का ज्यामितीय अर्थ

मान लीजिए फलन z = f (x , y) बिंदु a (x 0 , y 0) पर अवकलनीय है। इसका ग्राफ सतह है

एफ (एक्स, वाई) - जेड = 0।

चलो z 0 = f (x 0 , y 0) डालते हैं। तब बिंदु A (x 0 , y 0 , z 0) सतह से संबंधित है।

फलन F (x , y , z) = f (x , y) - z के आंशिक अवकलज हैं

F " x = f " x , F " y = f " y , F " z = − 1

और बिंदु A पर (x 0 , y 0 , z 0)

वे निरंतर हैं;
एफ "2 एक्स + एफ" 2 वाई + एफ "2 जेड = एफ" 2 एक्स + एफ "2 वाई + 1 ≠ 0।

अत: A, पृष्ठ F (x, y, z) का एक सामान्य बिंदु है और इस बिंदु पर सतह पर एक स्पर्श रेखा है। (3) के अनुसार, स्पर्शरेखा समतल समीकरण का रूप है:

f "x (x 0 , y 0 ) (x - x 0 ) + f " y (x 0 , y 0 ) (y - y 0 ) - (z - z 0 ) = 0।

बिंदु a (x 0, y 0) से एक मनमाना बिंदु p (x, y) में संक्रमण के दौरान स्पर्शरेखा तल पर एक बिंदु का ऊर्ध्वाधर विस्थापन B Q (चित्र 2) है। संबंधित एप्लिक इंक्रीमेंट है

(जेड - जेड 0) \u003d एफ "एक्स (एक्स 0, वाई 0) (एक्स - एक्स 0) + एफ" वाई (एक्स 0, वाई 0) (वाई - वाई 0)

यहाँ दायीं ओर अंतर है डीफ़ंक्शन z का z = f (x, y) बिंदु a (x 0 , x 0) पर। इसलिये,
डीएफ (एक्स 0, वाई 0)। फ़ंक्शन f (x, y) के बिंदु (x 0, y 0, z 0 = f (x 0, y 0)) के ग्राफ के लिए समतल स्पर्शरेखा के बिंदु के अनुप्रयोग की वृद्धि है।

यह अंतर की परिभाषा से निम्नानुसार है कि फ़ंक्शन के ग्राफ़ पर बिंदु P और स्पर्शरेखा तल पर बिंदु Q के बीच की दूरी बिंदु p से बिंदु a तक की दूरी की तुलना में एक अनंत उच्च क्रम है।

एक सतह को उन बिंदुओं के समूह के रूप में परिभाषित किया जाता है जिनके निर्देशांक एक निश्चित प्रकार के समीकरण को संतुष्ट करते हैं:

F (x , y , z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

यदि समारोह F (x , y , z) (\displaystyle F(x,\,y,\,z))किसी बिंदु पर निरंतर है और उस पर निरंतर आंशिक व्युत्पन्न है, जिनमें से कम से कम एक गायब नहीं होता है, तो इस बिंदु के आसपास के क्षेत्र में समीकरण (1) द्वारा दी गई सतह होगी सही सतह.

उपरोक्त के अतिरिक्त सेटिंग का निहित तरीका, सतह को परिभाषित किया जा सकता है स्पष्ट रूप से, यदि एक चर, उदाहरण के लिए, z, को अन्य के रूप में व्यक्त किया जा सकता है:

z = f (x , y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

अधिक सख्ती से, सादा सतह इकाई वर्ग के आंतरिक भाग की होमोमोर्फिक मानचित्रण (अर्थात एक-से-एक और परस्पर सतत मानचित्रण) की छवि है। इस परिभाषा को एक विश्लेषणात्मक अभिव्यक्ति दी जा सकती है।

मान लीजिए कि एक समतल पर एक आयताकार निर्देशांक प्रणाली u और v के साथ एक वर्ग दिया गया है, जिसके आंतरिक बिंदुओं के निर्देशांक असमानताओं को संतुष्ट करते हैं।< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

एक उदाहरण सरल सतहएक गोलार्द्ध है। पूरा क्षेत्र नहीं है सादा सतह. यह एक सतह की अवधारणा के एक और सामान्यीकरण की आवश्यकता है।

अंतरिक्ष का एक उपसमुच्चय जिसमें प्रत्येक बिंदु का एक पड़ोस होता है जो है सादा सतह, कहा जाता है सही सतह .

अंतर ज्यामिति में सतह

घुमावदार

कैटेनॉयड

मीट्रिक विशिष्ट रूप से सतह के आकार को निर्धारित नहीं करता है। उदाहरण के लिए, एक हेलिकॉइड और एक कैटेनॉइड के मेट्रिक्स, एक उपयुक्त तरीके से पैरामीटर किए गए, मेल खाते हैं, अर्थात, उनके क्षेत्रों के बीच एक पत्राचार होता है जो सभी लंबाई (आइसोमेट्री) को संरक्षित करता है। आइसोमेट्रिक ट्रांसफॉर्मेशन के तहत संरक्षित गुण कहलाते हैं आंतरिक ज्यामितिसतहें। आंतरिक ज्यामिति अंतरिक्ष में सतह की स्थिति पर निर्भर नहीं करती है और जब यह तनाव और संपीड़न के बिना मुड़ी होती है (उदाहरण के लिए, जब एक सिलेंडर शंकु में मुड़ा हुआ होता है) नहीं बदलता है।

मीट्रिक गुणांक ई , एफ , जी (\displaystyle ई,\ एफ,\ जी)न केवल सभी वक्रों की लंबाई निर्धारित करें, बल्कि सामान्य रूप से सतह के अंदर सभी मापों के परिणाम (कोण, क्षेत्र, वक्रता, आदि)। इसलिए, सब कुछ जो केवल मीट्रिक पर निर्भर करता है, आंतरिक ज्यामिति को संदर्भित करता है।

सामान्य और सामान्य खंड

सतह बिंदुओं पर सामान्य वैक्टर

एक सतह की मुख्य विशेषताओं में से एक इसकी है सामान्य- किसी दिए गए बिंदु पर स्पर्शरेखा विमान के लंबवत इकाई वेक्टर:

एम = [ आर यू , आर वी ′ ] | [ आर यू , आर वी ′ ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (आर"_(वी))]|))).

सामान्य का चिन्ह निर्देशांक की पसंद पर निर्भर करता है।

किसी दिए गए बिंदु पर सतह के अभिलंब वाले तल द्वारा सतह का खंड एक निश्चित वक्र बनाता है, जिसे कहा जाता है सामान्य खंडसतहें। एक सामान्य खंड के लिए मुख्य सामान्य सतह से सामान्य (एक संकेत तक) के साथ मेल खाता है।

यदि सतह पर वक्र एक सामान्य खंड नहीं है, तो इसका मुख्य सामान्य सतह के साथ एक कोण बनाता है (\displaystyle \थीटा ). फिर वक्रता k (\displaystyle k)वक्र वक्रता से संबंधित है k n (\displaystyle k_(n))सामान्य खंड (उसी स्पर्शरेखा के साथ) मेयुनियर का सूत्र:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

सतह को निर्दिष्ट करने के विभिन्न तरीकों के लिए सामान्य वेक्टर के निर्देशांक तालिका में दिए गए हैं:

	एक सतह बिंदु पर सामान्य निर्देशांक
निहित असाइनमेंट	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \ frac (\ आंशिक एफ) (\ आंशिक एक्स)); \, (\ फ्रैक (\ आंशिक एफ) (\ आंशिक वाई)); \, (\ फ्रैक (\ आंशिक एफ) (\ आंशिक जेड)) \ दाएं) )(\sqrt (\बाएं((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\बाएं((\frac (\आंशिक एफ)(\आंशिक जेड))\दाएं)^(2)))))
स्पष्ट असाइनमेंट	(- ∂ f ∂ x ; - ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f))) ) ( आंशिक x))\दाएं)^(2)+\बाएं ((\frac (\आंशिक च)(\आंशिक y))\दाएं)^(2)+1))))
पैरामीट्रिक कार्य	(डी (वाई, जेड) डी (यू, वी) डी (जेड, एक्स) डी (यू, वी) डी (एक्स, वाई) डी (यू, वी)) (डी (वाई, जेड) डी (यू , v)) 2 + (D (z , x) D (u , v)) 2 + (D (x , y) D (u , v)) 2 (\displaystyle (\frac (\left((\frac)) (डी(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\right)^(2 )+\बाएं ((\ फ्रैक (डी (जेड, एक्स)) (डी (यू, वी))) \ दाएं) ^ (2) + \ बाएं ((\ फ्रैक (डी (एक्स, वाई)) (डी ( यू, वी)))\दाएं)^(2)))))

यहां डी (वाई, जेड) डी (यू, वी) = | वाई यू वाई वी ′ जेड यू जेड वी ′ | , डी (जेड, एक्स) डी (यू, वी) = | जेड यू जेड वी ′ एक्स यू ′ एक्स वी ′ | , डी (एक्स, वाई) डी (यू, वी) = | एक्स यू एक्स वी ′ वाई यू वाई वी ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ start(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

सभी व्युत्पन्न बिंदु पर लिए जाते हैं (x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0))).

वक्रता

सतह पर किसी दिए गए बिंदु पर अलग-अलग दिशाओं के लिए, सामान्य खंड की एक अलग वक्रता प्राप्त होती है, जिसे कहा जाता है सामान्य वक्रता; यदि वक्र का मुख्य अभिलम्ब उसी दिशा में जाता है जिस दिशा में सतह पर जाता है, या ऋण चिह्न यदि मानक की दिशा विपरीत होती है तो इसे एक धन चिह्न दिया जाता है।

सामान्यतया, सतह पर प्रत्येक बिंदु पर दो लंबवत दिशाएँ होती हैं ई 1 (\displaystyle e_(1))और ई 2 (\displaystyle e_(2)), जिसमें सामान्य वक्रता न्यूनतम और अधिकतम मान लेती है; इन दिशाओं को कहा जाता है मुख्य. एक अपवाद तब होता है जब सामान्य वक्रता सभी दिशाओं में समान होती है (उदाहरण के लिए, एक गोले के पास या क्रांति के दीर्घवृत्त के अंत में), तो एक बिंदु पर सभी दिशाएँ प्रमुख होती हैं।

ऋणात्मक (बाएं), शून्य (केंद्र), और धनात्मक (दाएं) वक्रता वाली सतहें।

मुख्य दिशाओं में सामान्य वक्रता कहलाती है मुख्य वक्रता; आइए उन्हें निरूपित करें κ 1 (\displaystyle \कप्पा _(1))और κ 2 (\displaystyle \कप्पा _(2)). आकार:

के = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

किसी बिंदु पर और उस पर निरंतर आंशिक व्युत्पन्न है, जिनमें से कम से कम एक गायब नहीं होता है, तो इस बिंदु के आसपास के क्षेत्र में समीकरण (1) द्वारा दी गई सतह होगी सही सतह.

उपरोक्त के अतिरिक्त सेटिंग का निहित तरीकासतह को परिभाषित किया जा सकता है स्पष्ट रूप से, यदि एक चर, उदाहरण के लिए z, को अन्य के रूप में व्यक्त किया जा सकता है:

भी मौजूद है पैरामीट्रिकअसाइनमेंट विधि। इस मामले में, सतह समीकरणों की प्रणाली द्वारा निर्धारित की जाती है:

एक साधारण सतह की अवधारणा

अधिक सटीकता से, सादा सतह इकाई वर्ग के आंतरिक भाग की होमोमोर्फिक मानचित्रण (अर्थात एक-से-एक और परस्पर सतत मानचित्रण) की छवि है। इस परिभाषा को एक विश्लेषणात्मक अभिव्यक्ति दी जा सकती है।

अंतर ज्यामिति में सतह

घुमावदार

कैटेनॉयड

मीट्रिक गुणांक न केवल सभी वक्रों की लंबाई निर्धारित करते हैं, बल्कि सामान्य रूप से सतह (कोण, क्षेत्र, वक्रता, आदि) के अंदर सभी मापों के परिणाम निर्धारित करते हैं। इसलिए, सब कुछ जो केवल मीट्रिक पर निर्भर करता है, आंतरिक ज्यामिति को संदर्भित करता है।

सामान्य और सामान्य खंड

सतह बिंदुओं पर सामान्य वैक्टर

सामान्य का चिन्ह निर्देशांक की पसंद पर निर्भर करता है।

एक समतल द्वारा सतह का खंड जिसमें अभिलंब (किसी दिए गए बिंदु पर) होता है, सतह पर एक निश्चित वक्र बनाता है, जिसे कहा जाता है सामान्य खंडसतहें। एक सामान्य खंड के लिए मुख्य सामान्य सतह से सामान्य (एक संकेत तक) के साथ मेल खाता है।

यदि सतह पर वक्र एक सामान्य खंड नहीं है, तो इसका मुख्य सामान्य सतह के साथ कोण θ बनाता है। फिर वक्रता कवक्र वक्रता से संबंधित है क एनसामान्य खंड (उसी स्पर्शरेखा के साथ) मेयुनियर का सूत्र:

	एक सतह बिंदु पर सामान्य निर्देशांक
निहित असाइनमेंट
स्पष्ट असाइनमेंट
पैरामीट्रिक कार्य

वक्रता

सामान्यतया, सतह पर प्रत्येक बिंदु पर दो लंबवत दिशाएँ होती हैं इ 1 और इ 2 , जिसमें सामान्य वक्रता न्यूनतम और अधिकतम मान लेती है; इन दिशाओं को कहा जाता है मुख्य. एक अपवाद तब होता है जब सामान्य वक्रता सभी दिशाओं में समान होती है (उदाहरण के लिए, एक गोले के पास या क्रांति के दीर्घवृत्त के अंत में), तो एक बिंदु पर सभी दिशाएँ प्रमुख होती हैं।

ऋणात्मक (बाएं), शून्य (केंद्र), और धनात्मक (दाएं) वक्रता वाली सतहें।

मुख्य दिशाओं में सामान्य वक्रता कहलाती है मुख्य वक्रता; आइए उन्हें κ 1 और κ 2 से निरूपित करें। आकार:

क= 1 2

बुलाया गाऊसी वक्रता, पूर्ण वक्रताया केवल वक्रतासतहें। शब्द भी है वक्रता अदिश, जिसका अर्थ है वक्रता टेंसर के दृढ़ संकल्प का परिणाम; इस मामले में, वक्रता स्केलर गाऊसी वक्रता से दोगुना बड़ा है।

गाऊसी वक्रता की गणना मीट्रिक के रूप में की जा सकती है, और इसलिए यह सतहों की आंतरिक ज्यामिति का एक उद्देश्य है (ध्यान दें कि प्रमुख वक्रता आंतरिक ज्यामिति से संबंधित नहीं है)। वक्रता के संकेत से, आप सतह के बिंदुओं को वर्गीकृत कर सकते हैं (आकृति देखें)। विमान की वक्रता शून्य है। त्रिज्या R वाले एक गोले की वक्रता सर्वत्र बराबर होती है। निरंतर नकारात्मक वक्रता की एक सतह भी है - एक छद्ममंडल।

जियोडेसिक रेखाएं, जियोडेसिक वक्रता

सतह पर वक्र कहलाता है भूगणितीय रेखा, या केवल जियोडेटिक, यदि इसके सभी बिंदुओं पर वक्र का मुख्य अभिलंब सतह के अभिलंब से मेल खाता है। उदाहरण: एक समतल पर, जियोडेसिक्स सीधी रेखाएँ और रेखा खंड होंगे, एक गोले पर - बड़े वृत्त और उनके खंड।

समतुल्य परिभाषा: एक भूगणितीय रेखा के लिए, इसके मुख्य सामान्य का सन्निहित तल पर प्रक्षेपण शून्य वेक्टर है। यदि वक्र भूगणित नहीं है, तो निर्दिष्ट प्रक्षेपण गैर-शून्य है; इसकी लंबाई कहा जाता है भूगणित वक्रता क जीसतह पर वक्र। एक अनुपात है:

कहाँ पे कइस वक्र की वक्रता है, क एन- समान स्पर्शरेखा के साथ इसके सामान्य खंड की वक्रता।

जियोडेसिक रेखाएं आंतरिक ज्यामिति को संदर्भित करती हैं। हम उनके मुख्य गुणों को सूचीबद्ध करते हैं।

एक और केवल एक जियोडेसिक किसी दिए गए दिशा में सतह पर दिए गए बिंदु से होकर गुजरता है।
सतह के पर्याप्त रूप से छोटे क्षेत्र पर, दो बिंदुओं को हमेशा एक जियोडेसिक द्वारा जोड़ा जा सकता है, और इसके अलावा, केवल एक। व्याख्या: एक गोले पर, विपरीत ध्रुव अनंत संख्या में मेरिडियन से जुड़े होते हैं, और दो करीबी बिंदुओं को न केवल एक बड़े वृत्त के एक खंड द्वारा जोड़ा जा सकता है, बल्कि एक पूर्ण वृत्त के अतिरिक्त भी जोड़ा जा सकता है, ताकि केवल विशिष्टता देखी जा सके एक छोटे में।
जियोडेसिक सबसे छोटा है। अधिक सख्ती से: सतह के एक छोटे से टुकड़े पर, दिए गए बिंदुओं के बीच का सबसे छोटा रास्ता जियोडेसिक के साथ होता है।

वर्ग

सतह का एक अन्य महत्वपूर्ण गुण इसका है वर्ग, जिसकी गणना सूत्र द्वारा की जाती है: