Dotykové roviny hrajú v geometrii veľkú úlohu. Konštrukcia dotykových rovín z praktického hľadiska je dôležitá, pretože ich prítomnosť vám umožňuje určiť smer normály k povrchu v bode kontaktu. Tento problém je široko používaný v inžinierskej praxi. Dotykové roviny sa používajú aj na vytváranie náčrtov geometrických útvarov ohraničených uzavretými plochami. Teoreticky sa roviny dotýkajúce sa povrchu používajú v diferenciálnej geometrii na štúdium vlastností povrchu v oblasti dotykového bodu.

Základné pojmy a definície

Rovina dotýkajúca sa povrchu by sa mala považovať za hraničnú polohu roviny sečny (podobne ako priamka dotyčnica ku krivke, ktorá je tiež definovaná ako medzná poloha sečny).

Rovina dotyčnica k povrchu v danom bode na povrchu je množina všetkých priamok - dotyčníc vedených k povrchu cez daný bod.

V diferenciálnej geometrii je dokázané, že všetky dotyčnice k ploche nakreslenej v obyčajnom bode sú koplanárne (patria do rovnakej roviny).

Poďme zistiť, ako sa kreslí priamka dotýkajúca sa povrchu. Dotyčnica t k ploche β v bode M uvedenom na ploche (obr. 203) predstavuje hraničnú polohu sečny l j pretínajúcej plochu v dvoch bodoch (MM 1, MM 2, ..., MM n), keď priesečníky sa zhodujú (M ≡ M n , l n ≡ l M). Je zrejmé, že (M1, M2, ..., Mn) ∈ g, pretože g ⊂ β. Z vyššie uvedeného vyplýva nasledujúca definícia: dotyčnica k povrchu je priamka dotýkajúca sa akejkoľvek krivky patriacej k povrchu.

Keďže rovina je definovaná dvoma pretínajúcimi sa priamkami, na nastavenie roviny dotýkajúcej sa plochy v danom bode stačí nakresliť cez tento bod dve ľubovoľné priamky patriace ploche (najlepšie jednoduchého tvaru) a zostrojiť dotyčnice každý z nich v priesečníku týchto čiar. Zostrojené dotyčnice jednoznačne určujú dotyčnicovú rovinu. Vizuálne znázornenie držania roviny α, dotyčnice k povrchu β v danom bode M, je uvedené na obr. 204. Tento obrázok ukazuje aj normálu n k ploche β.

Normálou k povrchu v danom bode je priamka kolmá na dotykovú rovinu a prechádzajúca bodom dotyku.

Priamka priesečníka plochy rovinou prechádzajúcou normálou sa nazýva normálový rez plochy. V závislosti od typu povrchu môže mať dotyková rovina s povrchom jeden alebo viacero bodov (priamok). Priamka dotyku môže byť zároveň priesečníkom plochy s rovinou.

Existujú aj prípady, keď sú na povrchu body, kde nie je možné nakresliť dotyčnicu k povrchu; takéto body sa nazývajú singulárne. Ako príklad singulárnych bodov možno uviesť body patriace k vrcholovej hrane povrchu trupu alebo priesečník poludníka rotačnej plochy s jej osou, ak sa poludník a os nepretínajú vpravo. uhol.

Typy kontaktu závisia od charakteru zakrivenia povrchu.

zakrivenie povrchu

Problémy zakrivenia povrchu skúmal francúzsky matematik F. Dupin (1784-1873), ktorý navrhol vizuálny spôsob zobrazenia zmien zakrivenia normálnych častí povrchu.

Za týmto účelom sa v rovine dotýkajúcej sa uvažovaného povrchu v bode M (obr. 205, 206) na dotyčniciach k normálnym rezom na oboch stranách tohto bodu vykreslia segmenty rovné odmocninám hodnôt zodpovedajúce polomery zakrivenia týchto úsekov. Množina bodov – konce segmentov vymedzujú krivku tzv Dupinova indikatrix. Algoritmus na konštrukciu Dupinovej indikatrix (obr. 205) možno napísať:

1. M ∈ α, M ∈ β ∧ α β;

2. = √(Rl1), = √(Rl2),..., = √(Rln)

kde R je polomer zakrivenia.

(A 1 ∪ A 2 ∪ ... ∪ A n) je Dupinova indikatrix.

Ak je Dupinova indikatúra povrchu elipsa, potom sa bod M nazýva eliptický a povrch sa nazýva povrch s eliptickými bodmi.(obr. 206). V tomto prípade má dotyková rovina iba jeden spoločný bod s povrchom a všetky priamky patriace povrchu a pretínajúce sa v uvažovanom bode sú umiestnené na rovnakej strane dotykovej roviny. Príklady plôch s eliptickými bodmi sú: rotačný paraboloid, rotačný elipsoid, guľa (v tomto prípade Dupinova indikácia je kruh atď.).

Pri kreslení dotykovej roviny k povrchu trupu sa rovina dotkne tohto povrchu pozdĺž priamej tvoriacej čiary. Body tejto priamky sa nazývajú parabolický a povrch je povrch s parabolickými bodmi. Dupinova indikatrix sú v tomto prípade dve rovnobežné čiary (obr. 207*).

Na obr. 208 znázorňuje povrch pozostávajúci z bodov, v ktorých

* Krivka druhého rádu - parabola - sa za určitých podmienok môže rozpadnúť na dve skutočné rovnobežné priamky, dve imaginárne rovnobežky, dve zhodné priamky. Na obr. 207 máme do činenia s dvoma skutočnými rovnobežnými čiarami.

Voľná ​​dotyková rovina pretína povrch. Takýto povrch je tzv hyperbolický a body k tomu patriace - hyperbolické body. Dupinova indikatrix je v tomto prípade hyperbola.

Plocha, ktorej všetky body sú hyperbolické, má tvar sedla (šikmá rovina, jednovrstvový hyperboloid, konkávne rotačné plochy atď.).

Jedna plocha môže mať body rôzneho typu, napríklad na ploche trupu (obr. 209) je bod M eliptický; bod N - parabolický; bod K je hyperbolický.

V priebehu diferenciálnej geometrie sa dokázalo, že normálne úseky, v ktorých hodnoty zakrivenia Kj = 1/ Rj (kde Rj je polomer zakrivenia uvažovaného úseku) majú extrémne hodnoty, sa nachádzajú v dvoch vzájomne kolmé roviny.

Takéto zakrivenia K 1 = 1/R max. K 2 \u003d 1 / R min sa nazývajú hlavné a hodnoty H \u003d (K 1 + K 2) / 2 a K \u003d K 1 K 2 - priemerné zakrivenie povrch a celkové (Gaussovo) zakrivenie povrchu v uvažovanom bode. Pre eliptické body K > 0 je hyperbolický K

Nastavenie roviny dotyčnice k povrchu na Mongeovom diagrame

Nižšie si na konkrétnych príkladoch ukážeme konštrukciu rovinnej dotyčnice k ploche s eliptickými (príklad 1), parabolickými (príklad 2) a hyperbolickými (príklad 3) bodmi.

PRÍKLAD 1. Zostrojte rovinu α, dotýkajúcu sa rotačnej plochy β, s eliptickými bodmi. Zvážte dve možnosti riešenia tohto problému, a) bod M ∈ β ab) bod M ∉ β

Možnosť a (obr. 210).

Dotyková rovina je definovaná dvoma dotyčnicami t 1 a t 2 vedenými v bode M k rovnobežke a poludníku plochy β.

Priemet dotyčnice t 1 k rovnobežke h plochy β bude t" 1 ⊥ (S"M") a t" 1 || os x. Horizontálny priemet dotyčnice t "2 k poludníku d plochy β, prechádzajúcej bodom M, sa bude zhodovať s horizontálnym priemetom poludníka. Na nájdenie čelného priemetu dotyčnice t" 2 je poludníková rovina γ (γ ∋ M) otáčaním okolo osi plochy β sa prenesie do polohy γ 1 rovnobežnej s rovinou π 2 . V tomto prípade bod M → M 1 (M "1, M" 1). Priemet dotyčnice t "2 rarr; t" 2 1 je určený (M "1 S"). Ak teraz vrátime rovinu γ 1 do pôvodnej polohy, potom bod S "zostane na mieste (ako prislúchajúci osi rotácie) a M" 1 → M "a čelný priemet dotyčnice t" 2 zostane určiť (M "S")

Dve dotyčnice t 1 a t 2 pretínajúce sa v bode M ∈ β definujú rovinu α dotyčnicu k ploche β.

Možnosť b (obr. 211)

Na zostrojenie roviny dotyčnice k ploche prechádzajúcej bodom, ktorý nepatrí k ploche, treba vychádzať z nasledujúcich úvah: cez bod mimo plochy pozostávajúci z eliptických bodov možno nakresliť veľa rovín dotýkajúcich sa plochy. Obálka týchto plôch bude nejaká kužeľová plocha. Preto, ak neexistujú žiadne ďalšie indikácie, potom má problém veľa riešení a v tomto prípade sa redukuje na kreslenie kužeľovej plochy γ dotyčnice k danej ploche β.

Na obr. 211 je znázornená konštrukcia kužeľovej plochy γ dotyčnice ku gule β. Akákoľvek rovina α dotýkajúca sa kužeľovej plochy γ sa bude dotýkať plochy β.

Na zostrojenie priemetov plochy γ z bodov M "a M" nakreslíme dotyčnice kružníc h "a f" - priemetov gule. Označte dotykové body 1 (1" a 1"), 2 (2" a 2"), 3 (3" a 3") a 4 (4" a 4"). Horizontálny priemet kružnice - línia dotyku kužeľovej plochy a gule sa premietne do [ 1 "2"] Na nájdenie bodov elipsy, do ktorých sa táto kružnica premietne na čelnú rovinu priemetov použijeme rovnobežky gule.

Na obr. 211 týmto spôsobom sa určia čelné priemety bodov E a F (E "a F"). Ak máme kužeľovú plochu γ, zostrojíme k nej dotykovú rovinu α. Povaha a postupnosť grafiky

Niektoré z konštrukcií, ktoré je na to potrebné urobiť, sú znázornené v nasledujúcom príklade.

PRÍKLAD 2 Zostrojte rovinu α dotyčnicu k ploche β s parabolickými bodmi

Ako v príklade 1, uvažujme dve riešenia: a) bod N ∈ β; b) bod N ∉ β

Možnosť a (ryža 212).

Kužeľová plocha sa vzťahuje na plochy s parabolickými bodmi (pozri obr. 207.) Rovina dotýkajúca sa kužeľovej plochy sa jej dotýka pozdĺž priamočiarej tvoriacej priamky. Na jej zostrojenie musíte:

1) nakreslite tvoriacu čiaru SN (S"N" a S"N") cez daný bod N;

2) označte priesečník tvoriacej čiary (SN) s vodidlom d: (SN) ∩ d = A;

3) ťahajte a dotýkajte sa t k d v bode A.

Tvoriaca čiara (SA) a dotyčnica t, ktorá ju pretína, definujú rovinu α dotyčnicu ku kužeľovej ploche β v danom bode N*.

Vedenie roviny α dotýkajúcej sa kužeľovej plochy β a prechádzajúcej bodom N nepatrí

* Keďže plocha β pozostáva z parabolických bodov (okrem vrcholu S), rovina α, ktorá sa k nej dotýka, bude mať s ňou spoločný nie jeden bod N, ale priamku (SN).

lisovaním daného povrchu je potrebné:

1) daným bodom N a vrcholom S kužeľovej plochy β nakreslite priamku a (a "a");

2) určte vodorovnú stopu tejto priamky H a ;

3) nakreslite dotyčnice t "1 a t" 2 krivky h 0β až H a - vodorovná stopa kužeľovej plochy;

4) pripojte dotykové body A (A "a A") a B (B "a B") k vrcholu kužeľovej plochy S (S "a S").

Priesečníky t 1 , (AS) a t 2 , (BS) definujú požadované dotykové roviny α 1 a α 2

PRÍKLAD 3. Zostrojte rovinu α dotyčnicu k ploche β s hyperbolickými bodmi.

Bod K (obr. 214) sa nachádza na povrchu globoidu (vnútorný povrch prstenca).

Na určenie polohy dotykovej roviny α je potrebné:

1) nakreslite rovnobežku s povrchom β h(h", h") cez bod K;

2) nakreslite dotyčnicu cez bod K" t" 1 (t" 1 ≡ h");

3) na určenie smerov priemetov dotyčnice k poludníku je potrebné nakresliť rovinu γ cez bod K a os plochy, vodorovný priemet t "2 sa bude zhodovať s h 0γ; zostrojiť nárysnej priemete dotyčnice t" 2, najprv preložíme rovinu γ otáčaním okolo osi rotačnej plochy do polohy γ 1 || π 2. V tomto prípade sa poludníkový rez rovinou γ zhoduje s ľavým obrysovým oblúkom čelnej projekcie - polkruhom g".

Bod K (K", K"), patriaci krivke poludníka, sa posunie do polohy K 1 (K" 1, K" 1). Cez K" 1 nakreslíme nárysný priemet dotyčnice t" 2 1, zarovnaný s rovinou γ 1 || π 2 polohu a označíme bod jej priesečníka s nárysným priemetom osi rotácie S "1. Rovinu γ 1 vrátime do pôvodnej polohy, bod K" 1 → K "(bod S" 1 ≡ S ") Čelný priemet dotyčnice t" 2 je určený bodmi K" a S".

Dotyčnice t 1 a t 2 definujú požadovanú dotykovú rovinu α, ktorá pretína plochu β pozdĺž krivky l .

PRÍKLAD 4. Zostrojte rovinu α dotyčnicu k ploche β v bode K. Bod K sa nachádza na povrchu jednovrstvového rotačného hyperboloidu (obr. 215).

Tento problém možno vyriešiť pomocou algoritmu použitého v predchádzajúcom príklade, ale berúc do úvahy, že povrch jednovrstvového rotačného hyperboloidu je riadený povrch, ktorý má dve rodiny priamočiarych generátorov a každý z generátorov jednej rodiny pretína všetky generátory druhej rodiny (pozri § 32, obr. 138). Cez každý bod tejto plochy môžu byť nakreslené dve pretínajúce sa priamky - generátory, ktoré sa budú súčasne dotýkať plochy jednovrstvového rotačného hyperboloidu.

Tieto dotyčnice definujú dotyčnicovú rovinu, t.j. rovina dotyčnica k povrchu jednovrstvového rotačného hyperboloidu pretína tento povrch pozdĺž dvoch priamok g 1 a g 2 . Na zostrojenie priemetov týchto priamok stačí použiť vodorovný priemet bodu K na prenášanie dotyčníc t "1 a t" 2 k horizontále.

tal priemet kružnice d "2 - hrdlo plochy jednovrstvového rotačného hyperboloidu; určte body 1" a 2, v ktorých t "1 a t" 2 pretínajú jedno z povrchových vodidiel d 1. Z 1" a 2" nájdeme 1" a 2", ktoré spolu s K" určujú čelné priemety požadovaných čiar.

Stiahnite si z Depositfiles

4. TEÓRIA PLOCH.

4.1 ROVNICE PLOCH.

Povrch v 3D priestore možno definovať:

1) implicitne: F ( X , r , z ) =0 (4.1)

2) výslovne: z = f ( X , r ) (4.2)

3) parametricky: (4.3)

alebo:
(4.3’)

kde sú skalárne argumenty
niekedy nazývané krivočiare súradnice. Napríklad guľa
je vhodné nastaviť v sférických súradniciach:
.

4.2 DOTYČNÁ ROVINA A NORMÁLNA K POVRCHU.

Ak priamka leží na povrchu (4.1), potom súradnice jej bodov spĺňajú rovnicu povrchu:

Rozlíšením tejto identity dostaneme:

(4.4)

alebo
(4.4 ’ )

v každom bode krivky na povrchu. Vektor gradientu v nesingulárnych bodoch povrchu (v ktorých je funkcia (4.5) diferencovateľná a
) je kolmý na vektory dotyčníc k ľubovoľným čiaram na povrchu, t.j. môže byť použitý ako normálový vektor na formulovanie rovnice dotyčnicovej roviny v bode M 0 (X 0 , r 0 , z 0 ) povrchy

(4.6)

a ako smerový vektor v normálnej rovnici:

(4.7)

V prípade explicitného (4.2) priradenia povrchu majú rovnice dotyčnicovej roviny a normály tvar:

(4.8)

a
(4.9)

V parametrickom znázornení plochy (4.3) sú vektory
ležia v dotykovej rovine a rovnicu dotykovej roviny možno zapísať ako:

(4.10)

a ich vektorový súčin možno považovať za riadiaci normálny vektor:

a normálna rovnica môže byť napísaná ako:

(4.11)

kde
- hodnoty parametrov zodpovedajúce bodu M 0 .

V nasledujúcom texte sa obmedzíme na zváženie iba tých bodov povrchu, kde sú vektory

sa nerovnajú nule a nie sú rovnobežné.

Príklad 4.1 Zostavte rovnice dotykovej roviny a normály v bode M 0 (1,1,2) na povrch rotačného paraboloidu
.

Riešenie: Keďže paraboloidná rovnica je daná explicitne, podľa (4.8) a (4.9) musíme nájsť
v bode M 0 :

a v bode M 0
. Potom rovnica dotykovej roviny v bode M 0 bude mať tvar:

2(X -1)+2(r -1)-(z-2) = 0 alebo 2 X +2 r -z - 2=0 a normálna rovnica
.

Príklad 4.2 Zostavte rovnice dotyčnicovej roviny a normály v ľubovoľnom bode skrutkovice
, .

rozhodnutie. Tu ,

Rovnica dotykovej roviny:

alebo

Normálne rovnice:

.

4.3 PRVÁ KVADRATICKÁ FORMA POVRCHU.

Ak je povrch daný rovnicou

potom krivka
na to môže byť dané rovnicou
(4.12)

Polomerový vektorový diferenciál
pozdĺž krivky zodpovedajúcej posunutiu z bodu M 0 do blízkeho bodu M, sa rovná

(4.13)

Ako
je diferenciál oblúka krivky zodpovedajúci rovnakému posunutiu), potom

(4.14)

kde .

Výraz na pravej strane (4.14) sa nazýva prvý kvadratický tvar povrchu a hrá obrovskú úlohu v teórii povrchov.

Integračný diferenciálds v rozmedzí od t 0 (zodpovedá bodu M 0) až t (zodpovedá bodu M), získame dĺžku zodpovedajúceho segmentu krivky

(4.15)

Keď poznáme prvý kvadratický tvar povrchu, môžeme nájsť nielen dĺžky, ale aj uhly medzi krivkami.

Ak du , dv sú diferenciály krivočiarych súradníc zodpovedajúce nekonečne malému posunu pozdĺž jednej krivky a
— na druhej strane, berúc do úvahy (4.13):

(4.16)

Pomocou vzorca

(4.17)

prvá kvadratická forma umožňuje vypočítať plochu oblasti
povrchy.

Príklad 4.3 Na helikoide nájdite dĺžku špirály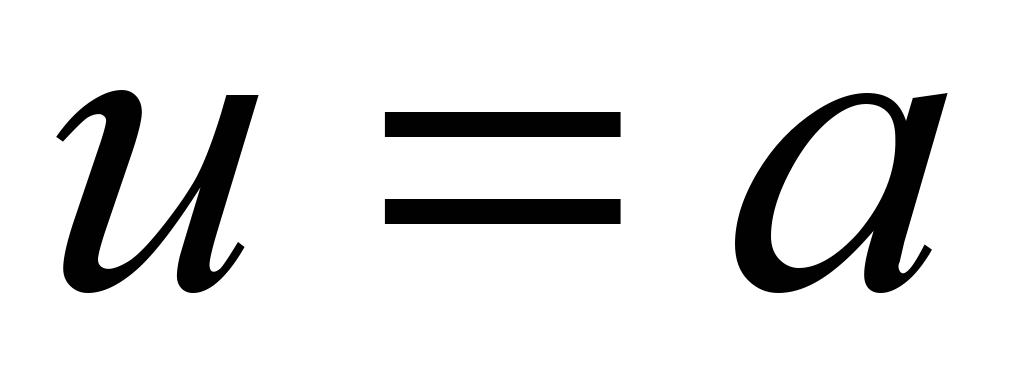
medzi dvoma bodmi.

rozhodnutie. Pretože na špirále
, potom . Nájdite v bode
prvá kvadratická forma. Označenie av = t , dostaneme rovnicu tejto skrutkovice v tvare . Kvadratický tvar:

= - prvá kvadratická forma.

Tu . V tomto prípade vo vzorci (4.15).
a dĺžka oblúka:

=

4.4 DRUHÝ KVADRATICKÝ FORMA POVRCHU.

Označiť
- jednotkový normálový vektor k povrchu
:

(4.18) . (4.23)

Čiara na povrchu sa nazýva čiara zakrivenia, ak jej smer v každom bode je hlavným smerom.

4.6 KONCEPCIA GEODETICKÝCH ČIAR NA POVRCHU.

Definícia 4.1 . Krivka na ploche sa nazýva geodetická, ak je jej hlavnou normálou v každom bode, kde je zakrivenie nenulové, sa zhoduje s normálom na povrch.

Cez každý bod povrchu v akomkoľvek smere prechádza a iba jeden geodetický. Napríklad na guli sú veľké kruhy geodetikou.

Parametrizácia povrchu sa nazýva semigeodetická, ak jedna skupina súradnicových čiar pozostáva z geodetických čiar a druhá je k nej ortogonálna. Napríklad na sférických meridiánoch (geodeziách) a rovnobežkách.

Geodézia na dostatočne malom segmente je najkratšia zo všetkých kriviek v jej blízkosti spájajúcich rovnaké body.

Rovnica normálnej roviny

1.

4.

Dotyková rovina a normála povrchu

Nech je daný nejaký povrch, A je pevný bod povrchu a B je premenný bod povrchu,

(obr. 1).

Nenulový vektor

→

n

volal normálny vektor na povrch v bode A ak

lim B→A j = π 2 .

Povrchový bod F (x, y, z) = 0 sa nazýva obyčajný, ak je v tomto bode

1. parciálne derivácie F " x , F " y , F " z sú spojité;
2. (F "x)2 + (F" y)2 + (F" z)2 ≠ 0.

Ak je porušená aspoň jedna z týchto podmienok, zavolá sa bod na povrchu singulárny bod povrchu .

Veta 1. Ak M(x 0 , y 0 , z 0 ) je obyčajný bod plochy F (x , y , z) = 0 , potom vektor

→ n \u003d grad F (x 0, y 0, z 0) \u003d F "x (x 0, y 0, z 0) → i + F "y (x 0, y 0, z 0) → j + F "z (x 0, y 0, z 0) → k

(1)

je kolmá na túto plochu v bode M (x 0 , y 0 , z 0 ) .

Dôkaz uvedený v knihe I.M. Petruško, L.A. Kuznecovová, V.I. Prokhorenko, V.F. Safonova ``Kurz vyššej matematiky: Integrálny počet. Funkcie viacerých premenných. Diferenciálne rovnice. M.: Vydavateľstvo MEI, 2002 (s. 128).

Normálne na povrch v určitom bode sa nazýva priamka, ktorej smerový vektor je v tomto bode kolmý na povrch a ktorá prechádza týmto bodom.

Kanonický normálne rovnice môže byť reprezentovaný ako

x - x0 F "x (x 0, y 0, z 0) = y – y0 F "y (x 0, y 0, z 0) = z−z0 F "z (x 0, y 0, z 0) .

(2)

Dotyková rovina k povrchu v určitom bode sa nazýva rovina, ktorá prechádza týmto bodom kolmá na normálu k povrchu v tomto bode.

Z tejto definície vyplýva, že rovnica dotykovej roviny vyzerá ako:

(3)

Ak je bod na povrchu singulárny, potom v tomto bode nemusí existovať kolmý vektor na povrch, a preto povrch nemusí mať normálnu a dotykovú rovinu.

Geometrický význam totálneho diferenciálu funkcie dvoch premenných

Nech je funkcia z = f (x , y) diferencovateľná v bode a (x 0 , y 0 ) . Jeho grafom je povrch

f (x, y) − z = 0.

Dajme z 0 = f (x 0 , y 0 ) . Potom bod A (x 0 , y 0 , z 0 ) patrí ploche.

Parciálne derivácie funkcie F (x , y , z) = f (x , y) − z sú

F " x = f " x , F " y = f " y , F " z = − 1

a v bode A (x 0 , y 0 , z 0 )

1. sú kontinuálne;
2. F "2 x + F "2 y + F "2 z = f "2 x + f "2 y + 1 ≠ 0 .

Preto je A obyčajný bod plochy F (x, y, z) av tomto bode je k ploche dotyková rovina. Podľa (3) má rovnica dotykovej roviny tvar:

f "x (x 0, y 0 ) (x − x 0 ) + f " y (x 0, y 0 ) (y − y 0 ) − (z − z 0 ) = 0.

Vertikálne posunutie bodu na dotykovej rovine pri prechode z bodu a (x 0 , y 0 ) do ľubovoľného bodu p (x , y) je B Q (obr. 2). Zodpovedajúci prírastok aplikácie je

(z - z 0 ) \u003d f "x (x 0, y 0) (x - x 0) + f" y (x 0, y 0) (y - y 0)

Tu na pravej strane je diferenciál d z funkcie z = f (x, y) v bode a (x 0 , x 0 ). teda
d f (x 0, y 0). je prírastok aplikácie bodu roviny dotyčnice ku grafu funkcie f (x, y) v bode (x 0, y 0, z 0 = f (x 0, y 0 )).

Z definície diferenciálu vyplýva, že vzdialenosť medzi bodom P na grafe funkcie a bodom Q na dotykovej rovine je nekonečne malý vyšší rád ako vzdialenosť bodu p k bodu a.

Povrch je definovaný ako množina bodov, ktorých súradnice spĺňajú určitý typ rovnice:

F (x, y, z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Ak je funkcia F (x, y, z) (\displaystyle F(x,\,y,\,z)) je v určitom bode spojitá a má v sebe spojité parciálne derivácie, z ktorých aspoň jedna nezaniká, potom v blízkosti tohto bodu bude plocha daná rovnicou (1) správny povrch.

Okrem vyššie uvedeného implicitný spôsob nastavenia, možno definovať povrch jasne, ak jednu z premenných, napríklad z, možno vyjadriť ako ostatné:

z = f (x, y) (1 ′) (\displaystyle z=f(x,y)\qquad (1“))

Prísnejšie, rovný povrch je obrazom homeomorfného zobrazenia (t. j. vzájomného súvislého zobrazenia jedna ku jednej) vnútra jednotkového štvorca. Táto definícia môže mať analytické vyjadrenie.

Nech je daný štvorec v rovine s pravouhlým súradnicovým systémom u a v , ktorého súradnice vnútorných bodov spĺňajú nerovnosti 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Príklad jednoduchý povrch je hemisféra. Celá oblasť nie je rovný povrch. To si vyžaduje ďalšie zovšeobecnenie pojmu povrch.

Podmnožina priestoru, v ktorej má každý bod susedstvo, ktoré je rovný povrch, sa volá správny povrch .

Povrch v diferenciálnej geometrii

Helicoid

katenoid

Metrika jednoznačne neurčuje tvar povrchu. Napríklad metriky helikoidu a katenoidu, parametrizované vhodným spôsobom, sa zhodujú, to znamená, že medzi ich oblasťami existuje zhoda, ktorá zachováva všetky dĺžky (izometria). Vlastnosti, ktoré sú zachované pri izometrických transformáciách, sa nazývajú vnútorná geometria povrchy. Vnútorná geometria nezávisí od polohy plochy v priestore a nemení sa pri jej ohýbaní bez napätia a stláčania (napríklad pri ohýbaní valca do kužeľa).

Metrické koeficienty E , F , G (\displaystyle E,\ F,\ G) určiť nielen dĺžky všetkých kriviek, ale vo všeobecnosti výsledky všetkých meraní vo vnútri povrchu (uhly, plochy, zakrivenie atď.). Preto všetko, čo závisí len od metriky, sa vzťahuje na vnútornú geometriu.

Normálny a normálny úsek

Normálne vektory v povrchových bodoch

Jednou z hlavných charakteristík povrchu je jeho normálne- jednotkový vektor kolmý na dotyčnú rovinu v danom bode:

m = [ r u′, r v′] | [ r u′ , r v ′ ] | (\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))).

Znak normály závisí od výberu súradníc.

Rez plochy rovinou obsahujúcou normálu plochy v danom bode tvorí určitú krivku, ktorá je tzv normálny úsek povrchy. Hlavná normála pre normálny úsek sa zhoduje s normálou k povrchu (až po znamienko).

Ak krivka na povrchu nie je normálnou sekciou, potom jej hlavná normála zviera uhol s normálou povrchu θ (\displaystyle \theta ). Potom zakrivenie k (\displaystyle k) krivka súvisí so zakrivením k n (\displaystyle k_(n)) normálny rez (s rovnakou dotyčnicou) Meunierov vzorec:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Súradnice normálového vektora pre rôzne spôsoby špecifikácie povrchu sú uvedené v tabuľke:

	Normálne súradnice v bode povrchu
implicitné zadanie	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\čiastočné F)(\čiastočné x));\,(\frac (\čiastočné F)(\čiastočné y));\,(\frac (\čiastočné F)(\čiastočné z))\vpravo) )(\sqrt (\vľavo((\frac (\čiastočné F)(\čiastočné x))\vpravo)^(2)+\vľavo((\frac (\čiastočné F)(\čiastočné y))\vpravo) ^(2)+\vľavo((\frac (\čiastočné F)(\čiastočné z))\vpravo)^(2)))))
explicitné zadanie	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\čiastočné f) )(\čiastočné x));\,-(\frac (\čiastočné f)(\čiastočné y));\,1\vpravo))(\sqrt (\vľavo((\frac (\čiastočné f)(\ čiastočné x))\vpravo)^(2)+\vľavo((\frac (\čiastočné f)(\čiastočné y))\vpravo)^(2)+1))))
parametrická úloha	(D (y, z) D (u, v); D (z, x) D (u, v); D (x, y) D (u, v)) (D (y, z) D (u , v)) 2 + (D (z , x) D (u, v)) 2 + (D (x, y) D (u, v)) 2 (\displaystyle (\frac (\left((\frac) (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x ,y))(D(u,v)))\right))(\sqrt (\left((\frac (D(y,z))(D(u,v)))\right)^(2 )+\left((\frac (D(z,x))(D(u,v)))\right)^(2)+\left((\frac (D(x,y))(D( u,v)))\vpravo)^(2)))))

Tu D (y, z) D (u, v) = | y u ′ y v ′ z u ′ z v “ | , D (z , x) D (u, v) = | z u ′ z v ′ x u ′ x v ′ | , D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ | (\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\začiatok(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatica)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))).

Všetky deriváty sa berú v bode (x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0))).

Zakrivenie

Pre rôzne smery v danom bode povrchu sa získa rôzne zakrivenie normálneho rezu, ktoré sa nazýva normálne zakrivenie; priradí sa jej znamienko plus, ak hlavná normála krivky ide v rovnakom smere ako normála k povrchu, alebo znamienko mínus, ak sú smery normály opačné.

Všeobecne povedané, v každom bode povrchu existujú dva kolmé smery e 1 (\displaystyle e_(1)) a e 2 (\displaystyle e_(2)), v ktorom normálne zakrivenie nadobúda minimálne a maximálne hodnoty; tieto smery sa nazývajú Hlavná. Výnimkou je prípad, keď je normálové zakrivenie rovnaké vo všetkých smeroch (napríklad v blízkosti gule alebo na konci rotačného elipsoidu), potom sú všetky smery v bode hlavné.

Plochy so záporným (vľavo), nulovým (v strede) a pozitívnym (vpravo) zakrivením.

Normálne zakrivenia v hlavných smeroch sa nazývajú hlavné zakrivenia; označme ich κ 1 (\displaystyle \kappa _(1)) a κ 2 (\displaystyle \kappa _(2)). Veľkosť:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

V určitom bode a má spojité parciálne derivácie, z ktorých aspoň jedna nezaniká, potom v blízkosti tohto bodu bude plocha daná rovnicou (1) správny povrch.

Okrem vyššie uvedeného implicitný spôsob nastavenia možno definovať povrch jasne, ak jednu z premenných, napríklad z, možno vyjadriť ako ostatné:

Tiež existuje parametrické spôsob priraďovania. V tomto prípade je povrch určený systémom rovníc:

Koncept jednoduchého povrchu

Presnejšie, rovný povrch je obrazom homeomorfného zobrazenia (t. j. vzájomného súvislého zobrazenia jedna ku jednej) vnútra jednotkového štvorca. Táto definícia môže mať analytické vyjadrenie.

Nech je daný štvorec v rovine s pravouhlým súradnicovým systémom u a v , ktorého súradnice vnútorných bodov spĺňajú nerovnosti 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Príklad jednoduchý povrch je hemisféra. Celá oblasť nie je rovný povrch. To si vyžaduje ďalšie zovšeobecnenie pojmu povrch.

Podmnožina priestoru, v ktorej má každý bod susedstvo, ktoré je rovný povrch, sa volá správny povrch .

Povrch v diferenciálnej geometrii

Helicoid

katenoid

Metrika jednoznačne neurčuje tvar povrchu. Napríklad metriky helikoidu a katenoidu, parametrizované vhodným spôsobom, sa zhodujú, to znamená, že medzi ich oblasťami existuje zhoda, ktorá zachováva všetky dĺžky (izometria). Vlastnosti, ktoré sú zachované pri izometrických transformáciách, sa nazývajú vnútorná geometria povrchy. Vnútorná geometria nezávisí od polohy plochy v priestore a nemení sa pri jej ohýbaní bez napätia a stláčania (napríklad pri ohýbaní valca do kužeľa).

Metrické koeficienty určujú nielen dĺžky všetkých kriviek, ale vo všeobecnosti výsledky všetkých meraní vo vnútri povrchu (uhly, plochy, zakrivenie atď.). Preto všetko, čo závisí len od metriky, sa vzťahuje na vnútornú geometriu.

Normálny a normálny úsek

Normálne vektory v povrchových bodoch

Jednou z hlavných charakteristík povrchu je jeho normálne- jednotkový vektor kolmý na dotyčnú rovinu v danom bode:

.

Znak normály závisí od výberu súradníc.

Rez plochy rovinou obsahujúcou normálu (v danom bode) tvorí na ploche určitú krivku, ktorá je tzv. normálny úsek povrchy. Hlavná normála pre normálny úsek sa zhoduje s normálou k povrchu (až po znamienko).

Ak krivka na povrchu nie je normálovým rezom, potom jej hlavná normála zviera s normálou povrchu uhol θ. Potom zakrivenie k krivka súvisí so zakrivením k n normálny rez (s rovnakou dotyčnicou) Meunierov vzorec:

Súradnice normálového vektora pre rôzne spôsoby špecifikácie povrchu sú uvedené v tabuľke:

	Normálne súradnice v bode povrchu
implicitné zadanie
explicitné zadanie
parametrická úloha

Zakrivenie

Pre rôzne smery v danom bode povrchu sa získa rôzne zakrivenie normálneho rezu, ktoré sa nazýva normálne zakrivenie; priradí sa jej znamienko plus, ak hlavná normála krivky ide v rovnakom smere ako normála k povrchu, alebo znamienko mínus, ak sú smery normály opačné.

Všeobecne povedané, v každom bode povrchu existujú dva kolmé smery e 1 a e 2, v ktorom má normálne zakrivenie minimálne a maximálne hodnoty; tieto smery sa nazývajú Hlavná. Výnimkou je prípad, keď je normálové zakrivenie rovnaké vo všetkých smeroch (napríklad v blízkosti gule alebo na konci rotačného elipsoidu), potom sú všetky smery v bode hlavné.

Plochy so záporným (vľavo), nulovým (v strede) a pozitívnym (vpravo) zakrivením.

Normálne zakrivenia v hlavných smeroch sa nazývajú hlavné zakrivenia; označme ich κ 1 a κ 2 . Veľkosť:

K= K 1 K 2

volal Gaussovo zakrivenie, plné zakrivenie alebo jednoducho zakrivenie povrchy. Existuje aj termín skalárne zakrivenie, čo znamená výsledok konvolúcie tenzora zakrivenia; v tomto prípade je skalárne zakrivenie dvakrát väčšie ako Gaussovo zakrivenie.

Gaussovo zakrivenie je možné vypočítať z hľadiska metriky, a preto je predmetom vnútornej geometrie povrchov (všimnite si, že hlavné zakrivenia nepatria do vnútornej geometrie). Podľa znamienka zakrivenia môžete klasifikovať body povrchu (pozri obrázok). Zakrivenie roviny je nulové. Zakrivenie gule s polomerom R sa všade rovná . Existuje aj povrch konštantného negatívneho zakrivenia - pseudosféra.

Geodetické čiary, geodetické zakrivenie

Krivka na ploche je tzv geodetická čiara, alebo jednoducho geodetický, ak sa vo všetkých jej bodoch hlavná normála ku krivke zhoduje s normálou k ploche. Príklad: na rovine budú geodetikou priame čiary a úsečky, na gule - veľké kruhy a ich segmenty.

Ekvivalentná definícia: pre geodetickú priamku je priemetom jej hlavnej normály na priľahlú rovinu nulový vektor. Ak krivka nie je geodetická, potom zadaná projekcia je nenulová; jeho dĺžka je tzv geodetické zakrivenie k g krivka na povrchu. Existuje pomer:

,

kde k je zakrivenie tejto krivky, k n- zakrivenie jeho normálového rezu s rovnakou dotyčnicou.

Geodetické čiary sa vzťahujú na vnútornú geometriu. Uvádzame ich hlavné vlastnosti.

• Cez daný bod na povrchu v danom smere prechádza jedna a len jedna geodetická.
• Na dostatočne malej ploche povrchu môžu byť geodetikou spojené vždy dva body a navyše iba jeden. Vysvetlenie: na guli sú protiľahlé póly spojené nekonečným počtom poludníkov a dva blízke body môžu byť spojené nielen segmentom veľkého kruhu, ale aj jeho pridaním do celého kruhu, takže sa pozoruje iba jedinečnosť. v malom.
• Geodetická je najkratšia. Presnejšie: na malom kúsku povrchu leží najkratšia cesta medzi danými bodmi pozdĺž geodézie.

Námestie

Ďalším dôležitým atribútom povrchu je jeho námestie, ktorý sa vypočíta podľa vzorca: