दशमलव के साथ संचालन। दशमलव विभाजन: नियम, उदाहरण, समाधान

107. जोड़ दशमलव भाग.

दशमलवों को जोड़ना उसी तरह से किया जाता है जैसे पूर्ण संख्याओं को जोड़ना। आइए इसे उदाहरणों के साथ देखें।

1) 0.132 + 2.354। आइए एक के नीचे एक शर्तों पर हस्ताक्षर करें।

यहां, 2 हजारवें के साथ 4 हजारवें के योग से, 6 हजारवां प्राप्त हुआ;
3 सौ और 5 सौ के योग में से 8 सौवां निकला;
1 दहाई को 3 दहाई के साथ जोड़ने से -4 दहाई और
2 पूर्णांकों के साथ 0 पूर्णांकों को जोड़ने से - 2 पूर्णांक।

2) 5,065 + 7,83.

दूसरे कार्यकाल में कोई हज़ारवां हिस्सा नहीं है, इसलिए यह महत्वपूर्ण है कि एक-दूसरे के तहत शर्तों पर हस्ताक्षर करते समय गलती न करें।

3) 1,2357 + 0,469 + 2,08 + 3,90701.

यहां, हजारवां जोड़ने पर, हमें 21 हजारवां मिलता है; हमने 1 को हजारवें भाग में लिखा, और 2 को सौवें में जोड़ा, इसलिए सौवें स्थान पर हमें निम्नलिखित पद मिले: 2 + 3 + 6 + 8 + 0; कुल मिलाकर, वे 19 सौवां हिस्सा देते हैं, हमने 9 को सौवें के तहत हस्ताक्षरित किया, और 1 को दसवें के रूप में गिना गया, आदि।

इस प्रकार, दशमलव अंशों को जोड़ते समय, निम्नलिखित क्रम का पालन किया जाना चाहिए: भिन्नों को एक दूसरे के नीचे हस्ताक्षरित किया जाता है ताकि सभी शब्दों में समान अंक एक दूसरे के नीचे हों और सभी अल्पविराम एक ही ऊर्ध्वाधर कॉलम में हों; कुछ पदों के दशमलव स्थानों के दाईं ओर, वे कम से कम मानसिक रूप से, इतनी संख्या में शून्य का गुणन करते हैं कि दशमलव बिंदु के बाद के सभी पदों में अंकों की संख्या समान होती है। फिर अंकों से जोड़ करें, से शुरू करें दाईं ओर, और परिणामी राशि में उसी लंबवत कॉलम में अल्पविराम लगाएं जिसमें वह इन शर्तों में है।

§ 108. दशमलव भिन्नों का घटाव।

दशमलव को घटाना उसी तरह से किया जाता है जैसे पूर्ण संख्याओं को घटाना। आइए इसे उदाहरणों के साथ दिखाते हैं।

1) 9.87 - 7.32। आइए मिन्यूएंड के तहत सबट्रेंड पर हस्ताक्षर करें ताकि एक ही अंक की इकाइयाँ एक दूसरे के नीचे हों:

2) 16.29 - 4.75। आइए मिन्यूएंड के तहत सबट्रेंड पर हस्ताक्षर करें, जैसा कि पहले उदाहरण में है:

दसवें को घटाने के लिए, 6 में से एक पूरी इकाई को लेकर उसे दसवें हिस्से में विभाजित करना होता था।

3) 14.0213-5.350712। आइए मिन्यूएंड के तहत सबट्रेंड पर हस्ताक्षर करें:

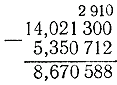
घटाव निम्नानुसार किया गया था: चूंकि हम 0 से 2 मिलियन नहीं घटा सकते हैं, हमें निकटतम अंक को बाईं ओर देखना चाहिए, यानी सौ-हजारवां, लेकिन सौ-हजारवें के स्थान पर शून्य भी है, इसलिए हम 1 लेते हैं 3 दस-हज़ारवें में से दस-हज़ार और हम इसे सौ-हज़ारवें हिस्से में विभाजित करते हैं, हमें 10 सौ-हज़ारवां मिलता है, जिसमें से 9 सौ-हज़ारवां सौ-हज़ारवें की श्रेणी में छोड़ दिया जाता है, और हम 1 सौ-हज़ारवें हिस्से को मिलियन में विभाजित करते हैं, हमें 10 मिलियन मिलते हैं। इस प्रकार, में पिछले तीनहमें मिले अंक: दस लाखवाँ, सौ-हज़ारवाँ 9, दस-हज़ारवाँ 2. अधिक स्पष्टता और सुविधा के लिए (भूलने के लिए नहीं), ये संख्याएँ कम के संगत भिन्नात्मक अंकों के ऊपर लिखी जाती हैं। अब हम घटाना शुरू कर सकते हैं। हम 10 मिलियन में से 2 मिलियन घटाते हैं, हमें 8 मिलियन मिलते हैं; 9 सौ-हजारवें में से 1 सौ-हजारवां घटाएं, हमें 8 सौ-हजारवां मिलता है, आदि।

इस प्रकार, दशमलव अंशों को घटाते समय, निम्नलिखित क्रम देखा जाता है: सबट्रेंड को कम के तहत हस्ताक्षरित किया जाता है ताकि समान अंक एक दूसरे के नीचे हों और सभी अल्पविराम एक ही ऊर्ध्वाधर कॉलम में हों; दाईं ओर, वे कम से कम मानसिक रूप से, कम या घटाए गए इतने शून्य में विशेषता रखते हैं ताकि उनके पास अंकों की समान संख्या हो, फिर अंकों से घटाएं, दाईं ओर से शुरू करें, और परिणामी अंतर में अल्पविराम लगाएं वही ऊर्ध्वाधर स्तंभ जिसमें यह कम और घटा में स्थित है।

109. दशमलव भिन्नों का गुणन।

दशमलव अंशों को गुणा करने के कुछ उदाहरणों पर विचार करें।

इन संख्याओं का गुणनफल ज्ञात करने के लिए, हम इस प्रकार तर्क कर सकते हैं: यदि गुणनखंड में 10 गुना वृद्धि की जाती है, तो दोनों गुणनखंड पूर्णांक होंगे और फिर हम पूर्णांकों को गुणा करने के नियमों के अनुसार उन्हें गुणा कर सकते हैं। लेकिन हम जानते हैं कि जब किसी एक कारक को कई गुना बढ़ाया जाता है, तो उत्पाद उसी मात्रा में बढ़ जाता है। इसका मतलब यह है कि संख्या जो पूर्णांक कारकों को गुणा करने के परिणामस्वरूप होती है, यानी 28 से 23, वास्तविक उत्पाद से 10 गुना अधिक है, और वास्तविक उत्पाद प्राप्त करने के लिए, आपको पाए गए उत्पाद को 10 गुना कम करना होगा। इसलिए, यहां आपको एक बार 10 से गुणा और एक बार 10 से भाग करना है, लेकिन कॉमा को एक चिह्न से दाएं और बाएं घुमाकर गुणा और 10 से भाग किया जाता है। इसलिए, आपको यह करने की आवश्यकता है: गुणक में, अल्पविराम को एक चिह्न से दाईं ओर ले जाएं, इससे यह 23 के बराबर होगा, फिर आपको परिणामी पूर्णांकों को गुणा करने की आवश्यकता है:

यह उत्पाद असली से 10 गुना बड़ा है। इसलिए, इसे 10 गुना कम किया जाना चाहिए, जिसके लिए हम अल्पविराम एक वर्ण को बाईं ओर ले जाते हैं। इस प्रकार, हम प्राप्त करते हैं

28 2,3 = 64,4.

सत्यापन उद्देश्यों के लिए, आप एक दशमलव अंश को हर के साथ लिख सकते हैं और साधारण अंशों को गुणा करने के लिए नियम के अनुसार एक क्रिया कर सकते हैं, अर्थात।

2) 12,27 0,021.

इस उदाहरण और पिछले उदाहरण के बीच का अंतर यह है कि यहां दोनों कारकों को दशमलव अंशों द्वारा दर्शाया गया है। लेकिन यहां, गुणा की प्रक्रिया में, हम अल्पविराम पर ध्यान नहीं देंगे, अर्थात, हम अस्थायी रूप से गुणक को 100 गुना और गुणक को 1,000 गुना बढ़ा देंगे, जिससे उत्पाद में 100,000 गुना वृद्धि होगी। इस प्रकार, 1227 को 21 से गुणा करने पर, हम प्राप्त करते हैं:

1 227 21 = 25 767.

यह मानते हुए कि परिणामी उत्पाद वास्तविक उत्पाद का 100,000 गुना है, अब हमें इसमें अल्पविराम लगाकर इसे 100,000 के कारक से कम करना चाहिए, फिर हमें मिलता है:

32,27 0,021 = 0,25767.

चलो देखते है:

इस प्रकार, दो दशमलव अंशों को गुणा करने के लिए, अल्पविराम पर ध्यान दिए बिना, उन्हें पूर्णांक के रूप में गुणा करने के लिए और उत्पाद में दाईं ओर अल्पविराम से अलग करने के लिए पर्याप्त है, जितने दशमलव स्थानों में और गुणक में थे एक साथ कारक।

अंतिम उदाहरण में, परिणाम पाँच दशमलव स्थानों वाला एक उत्पाद है। यदि इतनी अधिक सटीकता की आवश्यकता नहीं है, तो दशमलव अंश का पूर्णांकन किया जाता है। गोल करते समय, आपको उसी नियम का उपयोग करना चाहिए जो पूर्णांकों के लिए इंगित किया गया था।

110. तालिकाओं का उपयोग करके गुणा करना।

कभी-कभी तालिकाओं का उपयोग करके दशमलवों को गुणा किया जा सकता है। इस उद्देश्य के लिए, उदाहरण के लिए, आप दो अंकों की संख्याओं की उन गुणन सारणी का उपयोग कर सकते हैं, जिनका विवरण पहले दिया गया था।

1) 53 को 1.5 से गुणा करें।

हम 53 को 15 से गुणा करेंगे। तालिका में, यह उत्पाद 795 के बराबर है। हमने 53 का गुणनफल 15 पाया, लेकिन हमारा दूसरा कारक 10 गुना कम था, जिसका अर्थ है कि उत्पाद को 10 गुना कम करना होगा, अर्थात।

53 1,5 = 79,5.

2) 5.3 को 4.7 से गुणा करें।

सबसे पहले, हम तालिका में 53 का गुणन 47 पाते हैं, यह 2491 होगा। लेकिन चूंकि हमने गुणक और गुणक को कुल 100 गुना बढ़ा दिया है, तो परिणामी उत्पाद जितना होना चाहिए उससे 100 गुना बड़ा है; इसलिए हमें इस उत्पाद को 100 के कारक से कम करना होगा:

5,3 4,7 = 24,91.

3) 0.53 को 7.4 से गुणा करें।

पहले हम तालिका में 53 बटा 74 का गुणनफल पाते हैं; यह 3,922 होगा। लेकिन चूंकि हमने गुणक को 100 गुना और गुणक को 10 गुना बढ़ा दिया है, इसलिए गुणनफल में 1,000 गुना वृद्धि हुई है; इसलिए अब हमें इसे 1,000 के कारक से कम करना होगा:

0,53 7,4 = 3,922.

111. दशमलव का विभाजन।

हम इस क्रम में दशमलव भाग को देखेंगे:

1. दशमलव भाग द्वारा पूर्णांक,

1. दशमलव भिन्न का पूर्णांक से भाग।

1) 2.46 को 2 से भाग दें।

हम पहले 2 पूर्णांकों से विभाजित करते हैं, फिर दसवें और अंत में सौवें भाग से।

2) 32.46 को 3 से भाग दें।

32,46: 3 = 10,82.

हमने 3 दहाई को 3 से विभाजित किया, फिर हमने 2 इकाइयों को 3 से विभाजित करना शुरू किया; लाभांश की इकाइयों की संख्या के बाद से (2) कम भाजक(3) फिर मुझे भागफल में 0 लगाना था; इसके अलावा, शेष के लिए हमने 4 दहाई को ध्वस्त कर दिया और 24 दहाई को 3 से विभाजित कर दिया; निजी तौर पर 8 दसवें हिस्से में प्राप्त किया और अंत में 6 सौवें हिस्से में विभाजित किया।

3) 1.2345 को 5 से भाग दें।

1,2345: 5 = 0,2469.

यहाँ, भागफल में, पहले स्थान पर, शून्य पूर्णांक निकले, क्योंकि एक पूर्णांक 5 से विभाज्य नहीं है।

4) 13.58 को 4 से भाग दें।

इस उदाहरण की ख़ासियत यह है कि जब हमें निजी तौर पर 9 सौवां हिस्सा मिला, तो 2 सौवें के बराबर शेष मिला, हमने इस शेष को हजारवें हिस्से में विभाजित किया, 20 हजारवां हिस्सा मिला और विभाजन को अंत तक लाया।

नियम।एक पूर्णांक द्वारा दशमलव अंश का विभाजन उसी तरह किया जाता है जैसे पूर्णांकों का विभाजन, और परिणामी शेष दशमलव अंशों में परिवर्तित हो जाते हैं, अधिक से अधिक छोटे; विभाजन तब तक जारी रहता है जब तक शेष शून्य न हो जाए।

2. दशमलव भिन्न का दशमलव भिन्न से भाग।

1) 2.46 को 0.2 से विभाजित करें।

हम पहले से ही जानते हैं कि दशमलव अंश को पूर्णांक से कैसे विभाजित किया जाता है। आइए विचार करें कि क्या विभाजन के इस नए मामले को भी पिछले वाले तक कम किया जा सकता है? एक समय में, हमने भागफल की उल्लेखनीय संपत्ति पर विचार किया, जिसमें यह तथ्य शामिल है कि लाभांश और भाजक को समान संख्या में बढ़ाने या घटाने पर यह अपरिवर्तित रहता है। यदि भाजक एक पूर्णांक होता तो हम आसानी से हमें दी गई संख्याओं का विभाजन करते। ऐसा करने के लिए, इसे 10 गुना बढ़ाना पर्याप्त है, और सही भागफल प्राप्त करने के लिए, लाभांश को समान संख्या में, यानी 10 गुना बढ़ाना आवश्यक है। फिर इन संख्याओं के भाग को ऐसी संख्याओं के भाग से बदल दिया जाएगा:

और निजी तौर पर कोई संशोधन करने की आवश्यकता नहीं है।

आइए इस विभाजन को करें:

तो 2.46: 0.2 = 12.3.

2) 1.25 को 1.6 से भाग दें।

हम भाजक (1.6) को 10 गुना बढ़ाते हैं; ताकि भागफल न बदले, हम लाभांश को 10 गुना बढ़ा देते हैं; 12 पूर्णांक 16 से विभाज्य नहीं हैं, इसलिए हम भागफल 0 में लिखते हैं और 125 दहाई को 16 से विभाजित करते हैं, हमें भागफल में 7 दसवां भाग मिलता है और शेष 13 होता है। हम 13 दहाई को शून्य निर्दिष्ट करके सौवें में विभाजित करते हैं और 130 सौवें को 16 से विभाजित करते हैं, आदि। निम्नलिखित पर ध्यान दें:

a) जब भागफल में पूर्णांक प्राप्त नहीं होते हैं, तो उनके स्थान पर शून्य पूर्णांक लिखे जाते हैं;

b) जब लाभांश के अंक को शेष में लेने के बाद, एक संख्या प्राप्त होती है जो भाजक से विभाज्य नहीं होती है, तो भागफल में शून्य लिखा जाता है;

ग) जब, लाभांश के अंतिम अंक को हटा दिए जाने के बाद, विभाजन समाप्त नहीं होता है, तो शेष को शून्य देकर, विभाजन जारी रहता है;

d) यदि लाभांश एक पूर्णांक है, तो इसे दशमलव अंश से विभाजित करते समय, इसे शून्य देकर बढ़ाया जाता है।

इस प्रकार, किसी संख्या को दशमलव भिन्न से विभाजित करने के लिए, आपको भाजक में अल्पविराम को त्यागने की आवश्यकता है, और फिर भाजक को जितनी बार उसमें अल्पविराम गिरा दिया गया था, उतनी बार लाभांश बढ़ाना होगा, और फिर उसके अनुसार विभाजन करना होगा दशमलव अंश को एक पूर्णांक से विभाजित करने का नियम।

§ 112. अनुमानित भागफल।

पिछले पैराग्राफ में, हमने दशमलव अंशों के विभाजन पर विचार किया था, और हमारे द्वारा हल किए गए सभी उदाहरणों में, विभाजन को अंत तक लाया गया था, अर्थात, एक सटीक भागफल प्राप्त किया गया था। हालांकि, ज्यादातर मामलों में सटीक भागफल प्राप्त नहीं किया जा सकता है, भले ही हम विभाजन को कितनी दूर तक बढ़ा दें। ऐसा ही एक मामला है: 53 को 101 से भाग दें।

हम भागफल में पहले ही पाँच अंक प्राप्त कर चुके हैं, लेकिन विभाजन अभी समाप्त नहीं हुआ है और इसके कभी समाप्त होने की कोई आशा नहीं है, क्योंकि जो संख्याएँ हम पहले मिले हैं वे शेष में प्रकट होने लगती हैं। भागफल में भी संख्याएँ दोहराई जाएंगी: जाहिर है, संख्या 7 के बाद, संख्या 5 दिखाई देगी, फिर 2, और इसी तरह बिना अंत के। ऐसे मामलों में, विभाजन बाधित होता है और भागफल के पहले कुछ अंकों तक सीमित रहता है। इस निजी कहा जाता है अनुमानित।इस मामले में विभाजन कैसे करें, हम उदाहरणों के साथ दिखाएंगे।

मान लीजिए कि 25 को 3 से विभाजित करना आवश्यक है। यह स्पष्ट है कि पूर्णांक या दशमलव भिन्न के रूप में व्यक्त किया गया सटीक भागफल ऐसे विभाजन से प्राप्त नहीं किया जा सकता है। इसलिए, हम एक अनुमानित भागफल की तलाश करेंगे:

25: 3 = 8 और शेष 1

अनुमानित भागफल 8 है; यह, निश्चित रूप से, सटीक भागफल से कम है, क्योंकि 1 का शेष है। सटीक भागफल प्राप्त करने के लिए, आपको अनुमानित अनुमानित भागफल को जोड़ने की आवश्यकता है, अर्थात 8, वह अंश जो शेष को विभाजित करने के परिणामस्वरूप होता है , 1 के बराबर 3; यह अंश 1/3 होगा। इसका अर्थ है कि सटीक भागफल को मिश्रित संख्या 8 1 / 3 के रूप में व्यक्त किया जाएगा। चूँकि 1/3 एक उचित भिन्न है, अर्थात् एक भिन्न, एक से कम, फिर, इसे त्याग कर, हम मान लेते हैं गलती, कौन सा एक से कम. निजी 8 होगा एक नुकसान के साथ एक तक अनुमानित भागफल।अगर हम 8 के बजाय 9 लेते हैं, तो हम एक से कम त्रुटि की भी अनुमति देते हैं, क्योंकि हम पूरी इकाई नहीं, बल्कि 2/3 जोड़ देंगे। ऐसा निजी वसीयतनामा एक से अधिक के साथ अनुमानित भागफल।

आइए अब एक और उदाहरण लेते हैं। मान लीजिए कि 27 को 8 से विभाजित करना आवश्यक है। चूंकि यहां हमें पूर्णांक के रूप में व्यक्त किया गया सटीक भागफल नहीं मिलेगा, हम एक अनुमानित भागफल की तलाश करेंगे:

27: 8 = 3 और शेषफल 3.

यहां त्रुटि 3/8 है, यह एक से कम है, जिसका अर्थ है कि अनुमानित भागफल (3) एक दोष के साथ पाया जाता है। हम विभाजन जारी रखते हैं: हम शेष 3 को दसवें में विभाजित करते हैं, हमें 30 दसवां मिलता है; आइए उन्हें 8 से विभाजित करें।

हम तीसरे स्थान पर दसवें और शेष बी दसवें स्थान पर अकेले रहे। यदि हम विशेष रूप से संख्या 3.3 तक ही सीमित रहते हैं, और शेष 6 को छोड़ देते हैं, तो हम एक दसवें से कम त्रुटि की अनुमति देंगे। क्यों? क्योंकि सटीक भागफल तब प्राप्त होगा जब हम 3.3 में 6 दहाई को 8 से विभाजित करने का परिणाम जोड़ते हैं; इस भाग से 6/80 होगा, जो दसवें हिस्से से कम है। (जाँचें!) इस प्रकार, यदि हम भागफल में स्वयं को दसवें तक सीमित करते हैं, तो हम कह सकते हैं कि हमें भागफल मिल गया है एक दसवें के लिए सटीक(नुकसान के साथ)।

आइए एक और दशमलव स्थान खोजने के लिए भाग को जारी रखें। ऐसा करने के लिए, हम 6 दहाई को सौवें भाग में विभाजित करते हैं और 60 सौवां प्राप्त करते हैं; आइए उन्हें 8 से विभाजित करें।

निजी तौर पर तीसरे स्थान पर यह 7 और शेष 4 सौवें स्थान पर निकला; यदि हम उन्हें त्याग देते हैं, तो हम एक सौवें से कम की त्रुटि की अनुमति देते हैं, क्योंकि 4 सौवें भाग को 8 से विभाजित करने पर सौवें भाग से कम होता है। ऐसे मामलों में, भागफल पाया जाना कहा जाता है। एक सौवें तक सटीक(नुकसान के साथ)।

अब हम जिस उदाहरण पर विचार कर रहे हैं, उसमें आप दशमलव भिन्न के रूप में व्यक्त सटीक भागफल प्राप्त कर सकते हैं। ऐसा करने के लिए, यह अंतिम शेष, 4 सौवें, को हज़ारवें भाग में विभाजित करने और 8 से विभाजित करने के लिए पर्याप्त है।

हालांकि, अधिकांश मामलों में, एक सटीक भागफल प्राप्त करना असंभव है और किसी को खुद को इसके अनुमानित मूल्यों तक सीमित रखना होगा। अब हम ऐसे उदाहरण पर विचार करेंगे:

40: 7 = 5,71428571...

संख्या के अंत में बिंदु इंगित करते हैं कि विभाजन पूरा नहीं हुआ है, अर्थात समानता अनुमानित है। आम तौर पर अनुमानित समानता इस तरह लिखी जाती है:

40: 7 = 5,71428571.

हमने भागफल को आठ दशमलव स्थानों के साथ लिया। लेकिन अगर इतनी बड़ी सटीकता की आवश्यकता नहीं है, तो कोई अपने आप को भागफल के पूरे भाग तक सीमित कर सकता है, यानी संख्या 5 (अधिक सटीक, 6); अधिक सटीकता के लिए, दसवें को ध्यान में रखा जा सकता है और भागफल को 5.7 के बराबर लिया जा सकता है; यदि किसी कारण से यह सटीकता अपर्याप्त है, तो हम सौवें पर रुक सकते हैं और 5.71, आदि ले सकते हैं। आइए अलग-अलग भागफलों को लिखें और उन्हें नाम दें।

पहला अनुमानित भागफल एक 6 तक।

दूसरा » » » से दसवां 5.7.

तीसरा » » » एक सौवें 5.71 तक।

चौथा » » » 5.714 के एक हजारवें हिस्से तक।

इस प्रकार, कुछ की सटीकता के साथ अनुमानित भागफल खोजने के लिए, उदाहरण के लिए, तीसरा दशमलव स्थान (यानी, एक हजारवें तक), जैसे ही यह संकेत मिलता है, विभाजन रोक दिया जाता है। इस मामले में, किसी को 40 में निर्धारित नियम को याद रखना चाहिए।

113. ब्याज के लिए सबसे सरल समस्याएं।

दशमलव भिन्नों का अध्ययन करने के बाद, हम कुछ और प्रतिशत समस्याओं को हल करेंगे।

ये समस्याएँ उन समस्याओं के समान हैं जिन्हें हमने साधारण भिन्नों के विभाग में हल किया था; लेकिन अब हम सौवां अंश दशमलव भिन्न के रूप में लिखेंगे, अर्थात् स्पष्ट रूप से निर्दिष्ट हर के बिना।

सबसे पहले, आपको 100 के हर के साथ एक साधारण अंश से दशमलव अंश में आसानी से स्विच करने में सक्षम होने की आवश्यकता है। ऐसा करने के लिए, आपको अंश को हर से विभाजित करने की आवश्यकता है:

नीचे दी गई तालिका दर्शाती है कि कैसे % (प्रतिशत) चिह्न वाली संख्या को 100 के हर वाले दशमलव द्वारा प्रतिस्थापित किया जाता है:

आइए अब कुछ समस्याओं पर विचार करें।

1. किसी दी गई संख्या का प्रतिशत ज्ञात करना।

कार्य 1।एक गांव में केवल 1,600 लोग रहते हैं। बच्चों की संख्या विद्यालय युगका 25% है कुल गणनारहने वाले। इस गांव में कितने स्कूली बच्चे हैं?

इस समस्या में, आपको 1600 का 25% या 0.25 ज्ञात करना होगा। समस्या को गुणा करके हल किया जाता है:

1600 0.25 = 400 (बच्चे)।

अत: 1,600 का 25%, 400 है।

इस कार्य की स्पष्ट समझ के लिए, यह याद रखना उपयोगी है कि प्रत्येक सौ जनसंख्या पर 25 स्कूली बच्चे हैं। इसलिए, सभी स्कूली बच्चों की संख्या ज्ञात करने के लिए, आप पहले यह पता लगा सकते हैं कि संख्या 1600 (16) में कितने सैकड़ों हैं, और फिर 25 को सैकड़ों (25 x 16 = 400) की संख्या से गुणा करें। इस तरह आप समाधान की वैधता की जांच कर सकते हैं।

कार्य 2.बचत बैंक जमाकर्ताओं को सालाना आय का 2% देते हैं। जमाकर्ता को प्रति वर्ष कितनी आय प्राप्त होगी जिसने जमा किया है: ए) 200 रूबल? बी) 500 रूबल? ग) 750 रूबल? घ) 1000 रूबल?

सभी चार मामलों में, समस्या को हल करने के लिए, संकेतित राशियों के 0.02 की गणना करना आवश्यक होगा, अर्थात, इनमें से प्रत्येक संख्या को 0.02 से गुणा करना होगा। हो जाए:

क) 200 0.02 = 4 (रूबल),

बी) 500 0.02 = 10 (रूबल),

सी) 750 0.02 = 15 (रूबल),

घ) 1,000 0.02 = 20 (रूबल)।

इनमें से प्रत्येक मामले को निम्नलिखित विचारों द्वारा सत्यापित किया जा सकता है। बचत बैंक जमाकर्ताओं को आय का 2% यानी बचत में लगाई गई राशि का 0.02 देते हैं। यदि राशि 100 रूबल थी, तो इसका 0.02 2 रूबल होगा। इसका मतलब है कि हर सौ जमाकर्ता को 2 रूबल लाता है। आय। इसलिए, विचार किए गए प्रत्येक मामले में, यह पता लगाने के लिए पर्याप्त है कि दी गई संख्या में कितने सैकड़ों हैं, और सैकड़ों की इस संख्या से 2 रूबल गुणा करें। उदाहरण के लिए a) सैकड़ो 2, so

2 2 \u003d 4 (रूबल)।

उदाहरण में d) सैकड़ा 10 होता है, जिसका अर्थ है

2 10 \u003d 20 (रूबल)।

2. किसी संख्या को उसके प्रतिशत से ज्ञात करना।

कार्य 1।वसंत में, स्कूल ने 54 छात्रों को स्नातक किया, जो कुल छात्रों की संख्या का 6% है। पिछले शैक्षणिक वर्ष के दौरान स्कूल में कितने छात्र थे?

आइए पहले इस समस्या का अर्थ स्पष्ट करें। स्कूल ने 54 छात्रों को स्नातक किया, जो छात्रों की कुल संख्या का 6% है, या, दूसरे शब्दों में, स्कूल में सभी छात्रों का 6 सौवां (0.06) है। इसका मतलब है कि हम संख्या (54) और भिन्न (0.06) द्वारा व्यक्त छात्रों के भाग को जानते हैं, और इस अंश से हमें पूरी संख्या मिलनी चाहिए। इस प्रकार, हमारे सामने एक संख्या को उसके भिन्न (§ 90 p. 6) से खोजने की एक सामान्य समस्या है। इस प्रकार की समस्याओं को विभाजन द्वारा हल किया जाता है:

इसका मतलब है कि स्कूल में 900 छात्र थे।

ऐसी समस्याओं को उलटा समस्या हल करके जांचना उपयोगी है, यानी समस्या को हल करने के बाद, आपको कम से कम अपने दिमाग में, पहले प्रकार की समस्या को हल करना चाहिए (किसी दी गई संख्या का प्रतिशत ज्ञात करना): मिली संख्या लें ( 900) दिए गए हैं और इससे हल की गई समस्या में दर्शाए गए प्रतिशत का पता लगाएं, अर्थात्:

900 0,06 = 54.

कार्य 2.परिवार महीने के दौरान भोजन पर 780 रूबल खर्च करता है, जो कि पिता की मासिक आय का 65% है। उसकी मासिक आय ज्ञात कीजिए।

इस कार्य का अर्थ पिछले वाले के समान ही है। यह मासिक आय का हिस्सा देता है, जो रूबल (780 रूबल) में व्यक्त किया जाता है, और इंगित करता है कि यह हिस्सा कुल कमाई का 65% या 0.65 है। और वांछित पूरी कमाई है:

780: 0,65 = 1 200.

इसलिए, वांछित कमाई 1200 रूबल है।

3. संख्याओं का प्रतिशत ज्ञात करना।

कार्य 1।पर स्कूल पुस्तकालयकेवल 6,000 किताबें। इनमें गणित पर 1,200 किताबें हैं। पुस्तकालय में कुल पुस्तकों की संख्या का कितना प्रतिशत गणित की पुस्तकों से है?

हम पहले ही इस तरह की समस्याओं (§97) पर विचार कर चुके हैं और इस निष्कर्ष पर पहुंचे हैं कि दो संख्याओं के प्रतिशत की गणना करने के लिए, आपको इन संख्याओं का अनुपात ज्ञात करना होगा और इसे 100 से गुणा करना होगा।

हमारे कार्य में, हमें संख्या 1,200 और 6,000 का प्रतिशत ज्ञात करना है।

हम पहले उनका अनुपात ज्ञात करते हैं, और फिर इसे 100 से गुणा करते हैं:

इस प्रकार, संख्या 1,200 और 6,000 का प्रतिशत 20 है। दूसरे शब्दों में, गणित की पुस्तकें सभी पुस्तकों की कुल संख्या का 20% हैं।

जाँच करने के लिए, हम व्युत्क्रम समस्या को हल करते हैं: 6,000 में से 20% खोजें:

6 000 0,2 = 1 200.

कार्य 2.संयंत्र को 200 टन कोयला प्राप्त करना चाहिए। 80 टन पहले ही वितरित किया जा चुका है। संयंत्र को कितने प्रतिशत कोयले की आपूर्ति की गई है?

यह समस्या पूछती है कि एक संख्या (80) दूसरे (200) का कितना प्रतिशत है। इन संख्याओं का अनुपात 80/200 होगा। आइए इसे 100 से गुणा करें:

इसका मतलब है कि 40% कोयले की डिलीवरी हो चुकी है।

इस लेख में, हम दशमलव अंशों के साथ विभाजन के रूप में ऐसी महत्वपूर्ण क्रिया का विश्लेषण करेंगे। पहले हम तैयार करते हैं सामान्य सिद्धांत, तो हम विश्लेषण करेंगे कि कैसे दशमलव अंशों को एक कॉलम द्वारा अन्य भिन्नों और प्राकृतिक संख्याओं में सही ढंग से विभाजित किया जाए। इसके बाद, हम साधारण भिन्नों के विभाजन का दशमलव और इसके विपरीत विश्लेषण करेंगे, और अंत में हम देखेंगे कि 0, 1, 0, 01, 100, 10, आदि में समाप्त होने वाले भिन्नों को सही ढंग से कैसे विभाजित किया जाए।

यहां हम केवल सकारात्मक अंशों वाले मामलों को लेते हैं। यदि भिन्न से पहले कोई ऋण है, तो इसके साथ कार्य करने के लिए, आपको परिमेय और वास्तविक संख्याओं के विभाजन पर सामग्री का अध्ययन करने की आवश्यकता है।

यांडेक्स.आरटीबी आर-ए-339285-1

सभी दशमलव भिन्न, परिमित और आवर्त दोनों, केवल . हैं विशेष रूपसाधारण अंशों का अंकन। इसलिए, उन पर वही सिद्धांत लागू होते हैं जो उनके संगत साधारण भिन्नों पर लागू होते हैं। इस प्रकार, हम दशमलव अंशों को विभाजित करने की पूरी प्रक्रिया को कम करके उन्हें सामान्य अंशों से बदल देते हैं, इसके बाद हम पहले से ज्ञात विधियों द्वारा गणना करते हैं। आइए एक विशिष्ट उदाहरण लेते हैं।

उदाहरण 1

1.2 को 0.48 से भाग दें।

समाधान

हम दशमलव भिन्नों को साधारण भिन्नों के रूप में लिखते हैं। हम यह कर सकेंगे:

1 , 2 = 12 10 = 6 5

0 , 48 = 48 100 = 12 25 .

इस प्रकार, हमें 6 5 को 12 25 से भाग देना होगा। हमें यकीन है:

1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2

परिणामी अनुचित भिन्न से, आप पूरे भाग का चयन कर सकते हैं और प्राप्त कर सकते हैं मिश्रित संख्या 2 1 2, या आप इसे दशमलव अंश के रूप में प्रस्तुत कर सकते हैं ताकि यह मूल संख्याओं से मेल खाए: 5 2 \u003d 2, 5। यह कैसे करना है, हम पहले ही लिख चुके हैं।

उत्तर: 1 , 2: 0 , 48 = 2 , 5 .

उदाहरण 2

गणना करें कि कितने होंगे 0 , (504) 0 , 56 ।

समाधान

सबसे पहले, हमें एक आवधिक दशमलव अंश को एक साधारण अंश में बदलने की आवश्यकता है।

0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111

उसके बाद, हम अंतिम दशमलव भिन्न का दूसरे रूप में भी अनुवाद करेंगे: 0, 56 = 56 100। अब हमारे पास दो संख्याएँ हैं जिनके साथ हमारे लिए आवश्यक गणना करना आसान होगा:

0 , (504) : 1, 11 = 56 111: 56 100 = 56 111 100 56 = 100 111

हमारे पास एक परिणाम है कि हम दशमलव में भी बदल सकते हैं। ऐसा करने के लिए, कॉलम विधि का उपयोग करके अंश को हर से विभाजित करें:

उत्तर: 0 , (504) : 0 , 56 = 0 , (900) .

यदि, भाग के उदाहरण में, हम गैर-आवधिक दशमलव अंशों से मिले हैं, तो हम थोड़ा अलग तरीके से कार्य करेंगे। हम उन्हें सामान्य साधारण भिन्नों में नहीं ला सकते हैं, इसलिए विभाजित करते समय, हमें पहले उन्हें एक निश्चित अंक तक गोल करना होगा। यह क्रिया लाभांश और भाजक दोनों के साथ की जानी चाहिए: हम सटीकता के हितों में मौजूदा परिमित या आवधिक अंश को भी गोल करेंगे।

उदाहरण 3

ज्ञात कीजिए कि 0, 779 .../1, 5602 कितना होगा।

समाधान

सबसे पहले, हम दोनों भिन्नों को सौवां तक ​​पूर्णांकित करते हैं। इस प्रकार हम अनंत अनावर्ती भिन्नों से परिमित दशमलव की ओर बढ़ते हैं:

0 , 779 … ≈ 0 , 78

1 , 5602 ≈ 1 , 56

हम गणना जारी रख सकते हैं और अनुमानित परिणाम प्राप्त कर सकते हैं: 0, 779 ...: 1, 5602 0, 78: 1, 56 = 78100: 156100 = 78100 100156 = 78156 = 12 = 0.5।

परिणाम की सटीकता गोलाई की डिग्री पर निर्भर करेगी।

उत्तर: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .

एक प्राकृतिक संख्या को दशमलव से और इसके विपरीत कैसे विभाजित करें

इस मामले में विभाजन का दृष्टिकोण लगभग समान है: हम परिमित और आवधिक अंशों को साधारण अंशों से बदलते हैं, और अनंत गैर-आवधिक अंशों को पूर्णांकित करते हैं। आइए एक प्राकृत संख्या और एक दशमलव भिन्न के साथ विभाजन के उदाहरण से शुरू करें।

उदाहरण 4

2.5 को 45 से भाग दें।

समाधान

आइए 2, 5 को एक साधारण भिन्न के रूप में लाएं: 255 10 \u003d 51 2. इसके बाद, हमें इसे केवल एक प्राकृतिक संख्या से विभाजित करने की आवश्यकता है। हम पहले से ही जानते हैं कि यह कैसे करना है:

25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30

यदि हम परिणाम का दशमलव अंकन में अनुवाद करते हैं, तो हमें 0 , 5 (6) मिलता है।

उत्तर: 25 , 5: 45 = 0 , 5 (6) .

न केवल प्राकृतिक संख्याओं के लिए एक कॉलम द्वारा विभाजन की विधि अच्छी है। सादृश्य द्वारा, हम इसका उपयोग भिन्नों के लिए भी कर सकते हैं। नीचे हम इसके लिए किए जाने वाले कार्यों के अनुक्रम को इंगित करेंगे।

परिभाषा 1

दशमलव अंशों के कॉलम को प्राकृत संख्याओं से विभाजित करने के लिए, आपको यह करना होगा:

1. दाईं ओर दशमलव भिन्न में कुछ शून्य जोड़ें (विभाजन के लिए, हम उनमें से कोई भी संख्या जोड़ सकते हैं जिसकी हमें आवश्यकता है)।

2. एक एल्गोरिथम का उपयोग करते हुए एक दशमलव अंश को एक प्राकृत संख्या से विभाजित करें। जब भिन्न के पूर्णांक भाग का विभाजन समाप्त हो जाता है, तो हम परिणामी भागफल में अल्पविराम लगाते हैं और आगे की गणना करते हैं।

इस तरह के विभाजन का परिणाम या तो एक परिमित या अनंत आवधिक दशमलव अंश हो सकता है। यह शेष पर निर्भर करता है: यदि यह शून्य है, तो परिणाम परिमित होगा, और यदि शेष दोहराना शुरू करते हैं, तो उत्तर एक आवधिक भिन्न होगा।

आइए कुछ कार्यों को एक उदाहरण के रूप में लें और इन चरणों को विशिष्ट संख्याओं के साथ पूरा करने का प्रयास करें।

उदाहरण 5

गणना करें कि 65, 14 4 कितना होगा।

समाधान

हम कॉलम विधि का उपयोग करते हैं। ऐसा करने के लिए, भिन्न में दो शून्य जोड़ें और दशमलव भिन्न 65, 1400 प्राप्त करें, जो मूल के बराबर होगा। अब हम 4 से भाग देने के लिए एक कॉलम लिखते हैं:

परिणामी संख्या हमें आवश्यक पूर्णांक भाग को विभाजित करने का परिणाम होगी। हम अल्पविराम लगाते हैं, इसे अलग करते हैं, और जारी रखते हैं:

हम शून्य शेष पर पहुंच गए हैं, इसलिए विभाजन की प्रक्रिया पूरी हो गई है।

उत्तर: 65 , 14: 4 = 16 , 285 .

उदाहरण 6

164.5 को 27 से भाग दें।

समाधान

हम पहले भिन्नात्मक भाग को विभाजित करते हैं और प्राप्त करते हैं:

हम परिणामी आकृति को अल्पविराम से अलग करते हैं और विभाजित करना जारी रखते हैं:

हम देखते हैं कि शेषफल समय-समय पर दोहराने लगे और संख्या नौ, दो और पांच भागफल में बारी-बारी से आने लगीं। हम वहीं रुकेंगे और उत्तर को आवर्त भिन्न 6, 0 (925) के रूप में लिखेंगे।

उत्तर: 164 , 5: 27 = 6 , 0 (925) .

इस तरह के विभाजन को एक निजी दशमलव अंश और ऊपर वर्णित एक प्राकृतिक संख्या खोजने की प्रक्रिया में कम किया जा सकता है। ऐसा करने के लिए, हमें लाभांश और भाजक को 10, 100, आदि से गुणा करना होगा ताकि भाजक एक प्राकृतिक संख्या में बदल जाए। फिर हम क्रियाओं के उपरोक्त क्रम को करते हैं। विभाजन और गुणन के गुणों के कारण यह दृष्टिकोण संभव है। शाब्दिक रूप में, हमने उन्हें इस तरह लिखा है:

ए: बी = (ए 10): (बी 10), ए: बी = (ए 100): (बी 100) और इसी तरह।

आइए नियम तैयार करें:

परिभाषा 2

एक अंतिम दशमलव अंश को दूसरे से विभाजित करने के लिए, आपको यह करना होगा:

1. भाजक को प्राकृत संख्या में बदलने के लिए आवश्यक वर्णों की संख्या से भाजक और भाजक में अल्पविराम को दाईं ओर ले जाएं। यदि लाभांश में पर्याप्त संकेत नहीं हैं, तो हम इसमें दाईं ओर शून्य जोड़ते हैं।

2. उसके बाद, हम भिन्न को एक कॉलम द्वारा परिणामी प्राकृत संख्या से विभाजित करते हैं।

आइए एक विशिष्ट समस्या पर एक नज़र डालें।

उदाहरण 7

7, 287 को 2, 1 से भाग दें।

हल: भाजक को एक प्राकृत संख्या बनाने के लिए, हमें अल्पविराम एक वर्ण को दाईं ओर ले जाना होगा। इसलिए हम दशमलव भिन्न 72, 87 को 21 से विभाजित करने के लिए आगे बढ़े। आइए प्राप्त संख्याओं को एक कॉलम में लिखें और गणना करें

उत्तर: 7 , 287: 2 , 1 = 3 , 47

उदाहरण 8

16 , 3 0 , 021 की गणना करें।

समाधान

हमें अल्पविराम को तीन अंकों तक ले जाना होगा। इसके लिए भाजक में पर्याप्त अंक नहीं हैं, जिसका अर्थ है कि आपको अतिरिक्त शून्य का उपयोग करने की आवश्यकता है। हमें लगता है कि अंतिम परिणाम होगा:

हम अवशेष 4 , 19 , 1 , 10 , 16 , 13 की आवधिक पुनरावृत्ति देखते हैं। भागफल 1 , 9 , 0 , 4 , 7 और 5 दोहराता है। तब हमारा परिणाम आवर्त दशमलव 776 , (190476) है।

उत्तर: 16 , 3: 0 , 021 = 776 , (190476) ​​​​​​

हमारे द्वारा वर्णित विधि आपको इसके विपरीत करने की अनुमति देती है, अर्थात, एक प्राकृतिक संख्या को अंतिम दशमलव अंश से विभाजित करती है। आइए देखें कि यह कैसे किया जाता है।

उदाहरण 9

गणना करें कि कितने होंगे 3 5 , 4 ।

समाधान

जाहिर है, हमें एक वर्ण द्वारा अल्पविराम को दाईं ओर ले जाना होगा। उसके बाद हम 30 , 0 को 54 से भाग देना शुरू कर सकते हैं। आइए डेटा को एक कॉलम में लिखें और परिणाम की गणना करें:

शेषफल को दोहराने से हमें संख्या 0 , (5) प्राप्त होती है, जो एक आवर्त दशमलव है।

उत्तर: 3: 5 , 4 = 0 , (5) .

दशमलव को 1000, 100, 10, आदि से कैसे विभाजित करें।

साधारण अंशों को विभाजित करने के लिए पहले से ही अध्ययन किए गए नियमों के अनुसार, एक अंश को दसियों, सैकड़ों, हजारों में विभाजित करना इसे 1/1000, 1/100, 1/10, आदि से गुणा करने के समान है। यह विभाजन करने के लिए निकलता है, में ये मामलाबस अल्पविराम को अंकों की वांछित संख्या में ले जाएं। यदि स्थानांतरित करने के लिए संख्या में पर्याप्त मान नहीं हैं, तो आपको आवश्यक संख्या में शून्य जोड़ने की आवश्यकता है।

उदाहरण 10

तो, 56, 21: 10 = 5, 621, और 0, 32: 100,000 = 0, 0000032।

अनंत दशमलव के मामले में, हम ऐसा ही करते हैं।

उदाहरण 11

उदाहरण के लिए, 3 , (56) : 1000 = 0 , 003 (56) और 593 , 374 ...: 100 = 5 , 93374 ...।

दशमलव को 0.001, 0.01, 0.1, आदि से कैसे विभाजित करें।

उसी नियम का उपयोग करके, हम भिन्नों को निर्दिष्ट मानों से विभाजित भी कर सकते हैं। यह क्रिया क्रमशः 1000, 100, 10 से गुणा करने के समान होगी। ऐसा करने के लिए, हम समस्या की स्थितियों के आधार पर अल्पविराम को एक, दो या तीन अंकों में ले जाते हैं, और संख्या में पर्याप्त अंक नहीं होने पर शून्य जोड़ते हैं।

उदाहरण 12

उदाहरण के लिए, 5, 739: 0, 1 = 57, 39 और 0, 21: 0, 00001 = 21,000।

यह नियम अनंत दशमलव पर भी लागू होता है। हम आपको केवल यही सलाह देते हैं कि उत्तर में प्राप्त भिन्न की अवधि से सावधान रहें।

तो, 7 , 5 (716) : 0 , 01 = 757 , (167) , क्योंकि दशमलव संकेतन 7 , 5716716716 ... दो अंकों को दाईं ओर ले जाने के बाद, हमें 757, 167167 ...

यदि उदाहरण में हमारे पास गैर-आवधिक भिन्न हैं, तो सब कुछ सरल है: 394 , 38283 ... : 0 , 001 = 394382 , 83 ... ।

एक मिश्रित संख्या या एक सामान्य अंश को दशमलव से और इसके विपरीत कैसे विभाजित करें

हम इस क्रिया को साधारण भिन्नों के साथ संचालन में भी कम करते हैं। ऐसा करने के लिए, दशमलव संख्याओं को संबंधित साधारण भिन्नों से बदलें, और मिश्रित संख्या को अनुचित भिन्न के रूप में लिखें।

यदि हम एक गैर-आवधिक अंश को एक साधारण या मिश्रित संख्या से विभाजित करते हैं, तो हमें इसके विपरीत, प्रतिस्थापित करने की आवश्यकता होती है सामान्य अंशया उनके संगत दशमलव अंश के साथ एक मिश्रित संख्या।

यदि आप टेक्स्ट में कोई गलती देखते हैं, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएं

इस प्रकाश में दशमलव को विभाजित करने के उदाहरणों पर विचार करें।

उदाहरण।

दशमलव 1.2 को दशमलव 0.48 से भाग दें।

समाधान।

उत्तर:

1,2:0,48=2,5 .

उदाहरण।

आवर्त दशमलव 0.(504) को दशमलव 0.56 से भाग दें।

समाधान।

आइए आवधिक दशमलव अंश का एक साधारण में अनुवाद करें:। हम अंतिम दशमलव अंश 0.56 को एक साधारण में भी अनुवाद करते हैं, हमारे पास 0.56 \u003d 56/100 है। अब हम मूल दशमलव को विभाजित करने से साधारण भिन्नों को विभाजित करने की ओर बढ़ सकते हैं और गणना समाप्त कर सकते हैं: .

आइए परिणामी साधारण अंश को एक कॉलम में हर द्वारा अंश को विभाजित करके दशमलव अंश में अनुवाद करें:

उत्तर:

0,(504):0,56=0,(900) .

अनंत गैर-आवधिक दशमलव अंशों को विभाजित करने का सिद्धांतपरिमित और आवधिक दशमलव अंशों को विभाजित करने के सिद्धांत से भिन्न है, क्योंकि गैर-दोहराव वाले दशमलव अंशों को साधारण अंशों में परिवर्तित नहीं किया जा सकता है। अनंत गैर-आवधिक दशमलव अंशों का विभाजन परिमित दशमलव अंशों के विभाजन में घटा दिया जाता है, जिसके लिए इसे किया जाता है पूर्णांकन संख्याएक निश्चित स्तर तक। इसके अलावा, यदि उन संख्याओं में से एक जिसके साथ विभाजन किया जाता है, एक अंतिम या आवधिक दशमलव अंश है, तो इसे गैर-आवधिक दशमलव अंश के समान अंक में भी पूर्णांकित किया जाता है।

उदाहरण।

अनंत अनावर्ती दशमलव 0.779... को अंतिम दशमलव 1.5602 से विभाजित करें।

समाधान।

अनंत दशमलव अंशों को विभाजित करने से परिमित दशमलव अंशों को विभाजित करने के लिए सबसे पहले आपको दशमलव अंशों को गोल करने की आवश्यकता है। हम सौवें तक गोल कर सकते हैं: 0.779…≈0.78 और 1.5602≈1.56। इस प्रकार, 0.779…:1.5602≈0.78:1.56= 78/100:156/100=78/100 100/156= 78/156=1/2=0,5 .

उत्तर:

0,779…:1,5602≈0,5 .

एक प्राकृत संख्या को दशमलव भिन्न से विभाजित करना और इसके विपरीत

एक प्राकृतिक संख्या को एक दशमलव अंश से विभाजित करने और एक दशमलव अंश को एक प्राकृतिक संख्या से विभाजित करने के दृष्टिकोण का सार दशमलव अंशों को विभाजित करने के सार से अलग नहीं है। अर्थात्, परिमित और आवर्त भिन्नों को साधारण भिन्नों द्वारा प्रतिस्थापित किया जाता है, और अनंत गैर-आवधिक भिन्नों को गोल किया जाता है।

उदाहरण के लिए, एक दशमलव अंश को एक प्राकृत संख्या से विभाजित करने के उदाहरण पर विचार करें।

उदाहरण।

दशमलव भिन्न 25.5 को प्राकृत संख्या 45 से भाग दें।

समाधान।

दशमलव भिन्न 25.5 को साधारण भिन्न 255/10=51/2 से प्रतिस्थापित करते हुए, भाग को साधारण भिन्न को प्राकृतिक संख्या से विभाजित करने के लिए घटाया जाता है: . दशमलव संकेतन में परिणामी भिन्न 0.5(6) है।

उत्तर:

25,5:45=0,5(6) .

एक कॉलम द्वारा एक प्राकृतिक संख्या द्वारा दशमलव अंश का विभाजन

प्राकृतिक संख्याओं द्वारा अंतिम दशमलव अंशों का विभाजन आसानी से एक कॉलम द्वारा प्राकृतिक संख्याओं के एक कॉलम द्वारा विभाजन के साथ समानता से किया जाता है। यहाँ विभाजन नियम है।

प्रति एक दशमलव को एक प्राकृतिक संख्या से एक कॉलम से विभाजित करें, ज़रूरी:

• विभाज्य दशमलव अंश 0 में दाईं ओर कुछ अंक जोड़ें, (विभाजन के दौरान, यदि आवश्यक हो, तो आप किसी भी संख्या में शून्य जोड़ सकते हैं, लेकिन इन शून्यों की आवश्यकता नहीं हो सकती है);
• प्राकृतिक संख्याओं के एक स्तंभ द्वारा विभाजित करने के लिए सभी नियमों के अनुसार एक दशमलव अंश के एक स्तंभ द्वारा एक प्राकृतिक संख्या से विभाजन करें, लेकिन जब दशमलव अंश के पूर्णांक भाग का विभाजन पूरा हो जाता है, तो निजी में आपको करने की आवश्यकता होती है अल्पविराम लगाएं और विभाजन जारी रखें।

आइए तुरंत कहें कि एक परिमित दशमलव अंश को एक प्राकृतिक संख्या से विभाजित करने के परिणामस्वरूप, या तो एक अंतिम दशमलव अंश या एक अनंत आवधिक दशमलव अंश प्राप्त किया जा सकता है। दरअसल, 0 के अलावा विभाज्य अंश के सभी दशमलव स्थानों के विभाजन के बाद, हम या तो शेष 0 प्राप्त कर सकते हैं, और हमें अंतिम दशमलव अंश मिलेगा, या शेष समय-समय पर दोहराना शुरू हो जाएगा, और हमें आवधिक दशमलव मिलेगा अंश।

आइए उदाहरणों को हल करते समय दशमलव अंशों को एक कॉलम द्वारा प्राकृतिक संख्याओं में विभाजित करने की सभी पेचीदगियों से निपटें।

उदाहरण।

दशमलव 65.14 को 4 से भाग दें।

समाधान।

आइए एक दशमलव अंश को एक प्राकृतिक संख्या से एक कॉलम से विभाजित करते हैं। आइए 65.14 भिन्न के रिकॉर्ड में दाईं ओर शून्य का एक जोड़ा जोड़ें, जबकि हमें इसके बराबर दशमलव अंश 65.1400 (बराबर और असमान दशमलव भिन्न देखें) मिलता है। अब आप दशमलव अंश 65.1400 के पूर्णांक भाग को एक प्राकृतिक संख्या 4 से एक कॉलम से विभाजित करना शुरू कर सकते हैं:

यह दशमलव भिन्न के पूर्णांक भाग के विभाजन को पूरा करता है। यहां निजी तौर पर आपको दशमलव बिंदु डालने और विभाजन जारी रखने की आवश्यकता है:

हम 0 के शेष पर आ गए हैं, इस स्तर पर एक कॉलम द्वारा विभाजन समाप्त होता है। परिणामस्वरूप, हमारे पास 65.14:4=16.285 है।

उत्तर:

65,14:4=16,285 .

उदाहरण।

164.5 को 27 से भाग दें।

समाधान।

आइए एक दशमलव अंश को एक प्राकृतिक संख्या से एक कॉलम से विभाजित करें। पूर्णांक भाग को विभाजित करने के बाद, हमें निम्नलिखित चित्र प्राप्त होता है:

अब हम निजी तौर पर अल्पविराम लगाते हैं और एक कॉलम के साथ विभाजन जारी रखते हैं:

अब यह स्पष्ट रूप से देखा गया है कि 25, 7 और 16 के अवशेष दोहराने लगे हैं, जबकि संख्या 9, 2 और 5 को भागफल में दोहराया गया है। अतः दशमलव 164.5 को 27 से भाग देने पर हमें आवर्त दशमलव 6.0(925) प्राप्त होता है।

उत्तर:

164,5:27=6,0(925) .

एक कॉलम द्वारा दशमलव अंशों का विभाजन

एक दशमलव अंश को एक दशमलव भिन्न से विभाजित करके एक दशमलव अंश को एक प्राकृतिक संख्या से एक कॉलम द्वारा विभाजित किया जा सकता है। ऐसा करने के लिए, लाभांश और भाजक को ऐसी संख्या 10, या 100, या 1000, आदि से गुणा किया जाना चाहिए, ताकि भाजक एक प्राकृतिक संख्या बन जाए, और फिर एक प्राकृतिक संख्या से एक कॉलम से विभाजित हो जाए। हम भाग और गुणा के गुणों के कारण ऐसा कर सकते हैं, क्योंकि a:b=(a 10):(b 10) , a:b=(a 100):(b 100) इत्यादि।

दूसरे शब्दों में, अंतिम दशमलव को अंतिम दशमलव से विभाजित करने के लिए, जरुरत:

• भाजक और भाजक में, अल्पविराम को दशमलव बिंदु के बाद जितने वर्ण हैं, उतने वर्णों से दाईं ओर ले जाएँ, यदि एक ही समय में अल्पविराम को स्थानांतरित करने के लिए लाभांश में पर्याप्त वर्ण नहीं हैं, तो आपको जोड़ने की आवश्यकता है दाईं ओर शून्य की आवश्यक संख्या;
• उसके बाद, दशमलव भिन्न के एक स्तंभ द्वारा एक प्राकृत संख्या से भाग करें।

एक उदाहरण को हल करते समय, दशमलव अंश से विभाजित करने के लिए इस नियम के अनुप्रयोग पर विचार करें।

उदाहरण।

कॉलम डिवीजन 7.287 को 2.1 से करें।

समाधान।

आइए इन दशमलव अंशों में अल्पविराम को एक अंक दाईं ओर ले जाएं, यह हमें दशमलव अंश 7.287 को दशमलव अंश 2.1 से विभाजित करने से दशमलव अंश 72.87 को प्राकृतिक संख्या 21 से विभाजित करने की अनुमति देगा। आइए एक कॉलम से विभाजित करें:

उत्तर:

7,287:2,1=3,47 .

उदाहरण।

दशमलव 16.3 को दशमलव 0.021 से भाग दें।

समाधान।

लाभांश और भाजक में अल्पविराम को 3 अंकों से दाईं ओर ले जाएं। जाहिर है, भाजक में अल्पविराम को ले जाने के लिए पर्याप्त अंक नहीं हैं, तो आइए आवश्यक संख्या में शून्य को दाईं ओर जोड़ें। अब हम भिन्न 16300.0 के कॉलम को प्राकृत संख्या 21 से विभाजित करते हैं:

इस क्षण से, शेष 4, 19, 1, 10, 16 और 13 की पुनरावृत्ति शुरू हो जाती है, जिसका अर्थ है कि भागफल में 1, 9, 0, 4, 7 और 6 की संख्या भी दोहराई जाएगी। परिणामस्वरूप, हमें एक आवर्त दशमलव भिन्न 776,(190476) प्राप्त होता है।

उत्तर:

16,3:0,021=776,(190476) .

ध्यान दें कि स्वरित नियम आपको एक प्राकृतिक संख्या को अंतिम दशमलव अंश से एक कॉलम से विभाजित करने की अनुमति देता है।

उदाहरण।

प्राकृत संख्या 3 को दशमलव भिन्न 5.4 से भाग दें।

समाधान।

अल्पविराम 1 अंक को दाईं ओर ले जाने के बाद, हम संख्या 30.0 को 54 से विभाजित करते हैं। आइए एक कॉलम से विभाजित करें:
.

अनंत दशमलव अंशों को 10, 100, ... से विभाजित करते समय भी यह नियम लागू किया जा सकता है। उदाहरण के लिए, 3,(56):1000=0.003(56) और 593.374…:100=5.93374…।

दशमलव को 0.1, 0.01, 0.001, आदि से विभाजित करना।

चूंकि 0.1 \u003d 1/10, 0.01 \u003d 1/100, आदि, यह एक साधारण अंश द्वारा विभाजन के नियम का अनुसरण करता है जो दशमलव अंश को 0.1, 0.01, 0.001, आदि से विभाजित करता है। । यह दिए गए दशमलव को 10 , 100 , 1000 , आदि से गुणा करने जैसा है। क्रमश।

दूसरे शब्दों में, दशमलव अंश को 0.1, 0.01, ... से विभाजित करने के लिए, आपको अल्पविराम को 1, 2, 3, ... अंकों से दाईं ओर ले जाना होगा, और यदि दशमलव अंश में पर्याप्त अंक नहीं हैं अल्पविराम को स्थानांतरित करें, फिर आपको आवश्यक संख्या को दाएं शून्य में जोड़ना होगा।

उदाहरण के लिए, 5.739:0.1=57.39 और 0.21:0.00001=21,000।

अनंत दशमलव को 0.1, 0.01, 0.001, आदि से विभाजित करते समय भी यही नियम लागू किया जा सकता है। इस मामले में, आपको आवधिक अंशों के विभाजन के साथ बहुत सावधान रहना चाहिए, ताकि विभाजन के परिणामस्वरूप प्राप्त अंश की अवधि के साथ गलत न हो। उदाहरण के लिए, 7.5(716):0.01=757,(167) , दशमलव अंश में अल्पविराम को 7.5716716716 ... दाईं ओर दो अंक ले जाने के बाद, हमारे पास रिकॉर्ड 757.167167 ... है। अनंत गैर-आवधिक दशमलव के साथ, सब कुछ सरल है: 394,38283…:0,001=394382,83… .

एक भिन्न या मिश्रित संख्या को दशमलव से विभाजित करना और इसके विपरीत

एक साधारण अंश या एक मिश्रित संख्या का एक परिमित या आवधिक दशमलव अंश द्वारा विभाजन, साथ ही एक परिमित या आवधिक दशमलव अंश का एक साधारण अंश या एक मिश्रित संख्या से विभाजन, साधारण अंशों के विभाजन के लिए कम हो जाता है। ऐसा करने के लिए, दशमलव अंशों को संबंधित साधारण अंशों से बदल दिया जाता है, और मिश्रित संख्या को एक अनुचित अंश के रूप में दर्शाया जाता है।

एक अनंत गैर-आवधिक दशमलव अंश को एक साधारण भिन्न या एक मिश्रित संख्या से विभाजित करते समय और इसके विपरीत, किसी को दशमलव अंशों को विभाजित करने के लिए आगे बढ़ना चाहिए, साधारण अंश या मिश्रित संख्या को संबंधित दशमलव अंश से बदलना चाहिए।

ग्रंथ सूची।

• गणित: अध्ययन करते हैं। 5 कोशिकाओं के लिए। सामान्य शिक्षा संस्थान / एन। हां। विलेनकिन, वी। आई। झोखोव, ए। एस। चेस्नोकोव, एस। आई। श्वार्ट्सबर्ड। - 21 वां संस्करण।, मिटा दिया गया। - एम .: मेनेमोसिन, 2007. - 280 पी .: बीमार। आईएसबीएन 5-346-00699-0।
• गणित।ग्रेड 6: पाठ्यपुस्तक। सामान्य शिक्षा के लिए संस्थान / [एन. हां। विलेनकिन और अन्य]। - 22वां संस्करण, रेव. - एम .: मेनेमोसिन, 2008. - 288 पी .: बीमार। आईएसबीएन 978-5-346-00897-2।
• बीजगणित:पाठयपुस्तक 8 कोशिकाओं के लिए। सामान्य शिक्षा संस्थान / [यू. एन। मकारिचेव, एन। जी। मिंड्युक, के। आई। नेशकोव, एस। बी। सुवोरोवा]; ईडी। एस ए तेल्याकोवस्की। - 16वां संस्करण। - एम।: शिक्षा, 2008। - 271 पी। : बीमार। - आईएसबीएन 978-5-09-019243-9।
• गुसेव वी.ए., मोर्दकोविच ए.जी.गणित (तकनीकी स्कूलों के आवेदकों के लिए एक मैनुअल): प्रोक। भत्ता।- एम।; उच्चतर स्कूल, 1984.-351 पी।, बीमार।

इस ट्यूटोरियल में, हम इनमें से प्रत्येक ऑपरेशन को एक-एक करके देखेंगे।

पाठ सामग्री

दशमलव जोड़ना

जैसा कि हम जानते हैं, दशमलव में एक पूर्णांक भाग और एक भिन्नात्मक भाग होता है। दशमलव जोड़ते समय, पूर्णांक और भिन्नात्मक भागों को अलग-अलग जोड़ा जाता है।

उदाहरण के लिए, आइए दशमलव 3.2 और 5.3 जोड़ें। किसी कॉलम में दशमलव भिन्नों को जोड़ना अधिक सुविधाजनक होता है।

सबसे पहले, हम इन दो अंशों को एक कॉलम में लिखते हैं, जबकि पूर्णांक भागों को पूर्णांक भागों के नीचे होना चाहिए, और भिन्नात्मक अंशों के नीचे होना चाहिए। स्कूल में, इस आवश्यकता को कहा जाता है "अल्पविराम के तहत अल्पविराम".

आइए भिन्नों को एक कॉलम में लिखें ताकि अल्पविराम अल्पविराम के नीचे हो:

हम भिन्नात्मक भागों को जोड़ना शुरू करते हैं: 2 + 3 \u003d 5. हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम पूर्णांक भागों को जोड़ते हैं: 3 + 5 = 8. हम अपने उत्तर के पूर्णांक भाग में आठ लिखते हैं:

अब हम पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करते हैं। ऐसा करने के लिए, हम फिर से नियम का पालन करते हैं "अल्पविराम के तहत अल्पविराम":

उत्तर मिला 8.5. तो व्यंजक 3.2 + 5.3 8.5 . के बराबर है

वास्तव में, सब कुछ उतना सरल नहीं है जितना पहली नज़र में लगता है। यहां भी, नुकसान हैं, जिनके बारे में हम अब बात करेंगे।

दशमलव में स्थान

सामान्य संख्याओं की तरह दशमलव के भी अपने अंक होते हैं। ये दसवें स्थान, सौवें स्थान, हजारवें स्थान हैं। इस मामले में, अंक दशमलव बिंदु के बाद शुरू होते हैं।

दशमलव बिंदु के बाद पहला अंक दसवें स्थान के लिए जिम्मेदार है, दूसरा अंक दशमलव बिंदु के बाद सौवें स्थान के लिए, तीसरा अंक दशमलव बिंदु के बाद हजारवें स्थान के लिए है।

दशमलव भिन्न में अंक कुछ जमा करते हैं उपयोगी जानकारी. विशेष रूप से, वे रिपोर्ट करते हैं कि दशमलव में कितने दसवें, सौवें और हज़ारवें हिस्से हैं।

उदाहरण के लिए, दशमलव 0.345 . पर विचार करें

वह स्थान जहाँ त्रिगुण स्थित होता है, कहलाता है दसवां स्थान

वह स्थान जहाँ चार स्थित होते हैं, कहलाते हैं सौवां स्थान

वह स्थान जहाँ पाँच स्थित होते हैं, कहलाते हैं हजारवें

आइए इस आंकड़े को देखें। हम देखते हैं कि दसवीं की श्रेणी में एक तीन है। इससे पता चलता है कि दशमलव भिन्न 0.345 में तीन दहाई होते हैं।

यदि हम भिन्नों को जोड़ते हैं, और फिर हमें मूल दशमलव भिन्न 0.345 . प्राप्त होता है

यह देखा जा सकता है कि पहले तो हमें इसका उत्तर मिला, लेकिन इसे दशमलव भिन्न में बदलकर 0.345 प्राप्त किया।

दशमलव भिन्नों को जोड़ते समय सामान्य संख्याओं को जोड़ने के समान सिद्धांतों और नियमों का पालन किया जाता है। दशमलव अंशों का जोड़ अंकों से होता है: दसवें को दसवें, सौवें से सौवें, हज़ारवें से हज़ारवें भाग में जोड़ा जाता है।

अतः दशमलव भिन्नों को जोड़ते समय नियम का पालन करना आवश्यक है "अल्पविराम के तहत अल्पविराम". अल्पविराम के तहत अल्पविराम वही क्रम प्रदान करता है जिसमें दसवें को दसवें, सौवें से सौवें, हज़ारवें से हज़ारवें भाग में जोड़ा जाता है।

उदाहरण 1व्यंजक 1.5 + 3.4 . का मान ज्ञात कीजिए

सबसे पहले, हम भिन्नात्मक भाग 5 + 4 = 9 जोड़ते हैं। हम अपने उत्तर के भिन्नात्मक भाग में नौ लिखते हैं:

अब हम पूर्णांक भागों 1 + 3 = 4 को जोड़ते हैं। हम अपने उत्तर के पूर्णांक भाग में चारों को लिखते हैं:

अब हम पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करते हैं। ऐसा करने के लिए, हम फिर से "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हैं:

उत्तर मिला 4.9. अतः व्यंजक 1.5 + 3.4 का मान 4.9 . है

उदाहरण 2व्यंजक का मान ज्ञात कीजिए: 3.51 + 1.22

हम इस अभिव्यक्ति को "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं।

सबसे पहले, भिन्नात्मक भाग, अर्थात् सौवां 1+2=3 जोड़ें। हम अपने उत्तर के सौवें भाग में त्रिक लिखते हैं:

अब 5+2=7 का दसवां हिस्सा जोड़ें। हम अपने उत्तर के दसवें भाग में सात लिखते हैं:

अब सारे भाग 3+1=4 जोड़ें। हम अपने उत्तर के पूरे भाग में चार लिखते हैं:

हम "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए पूर्णांक भाग को अल्पविराम से अलग करते हैं:

उत्तर मिला 4.73। अतः व्यंजक 3.51 + 1.22 का मान 4.73 . है

3,51 + 1,22 = 4,73

सामान्य संख्याओं की तरह, दशमलव भिन्नों को जोड़ते समय, . इस मामले में, एक अंक उत्तर में लिखा जाता है, और बाकी को अगले अंक में स्थानांतरित कर दिया जाता है।

उदाहरण 3व्यंजक का मान ज्ञात कीजिए 2.65 + 3.27

हम इस अभिव्यक्ति को एक कॉलम में लिखते हैं:

5+7=12 का सौवां भाग जोड़ें। हमारे उत्तर के सौवें भाग में संख्या 12 फिट नहीं होगी। इसलिए, सौवें भाग में, हम संख्या 2 लिखते हैं, और इकाई को अगले बिट में स्थानांतरित करते हैं:

अब हम 6+2=8 के दहाई को जोड़ते हैं और पिछले ऑपरेशन से हमें जो इकाई मिली है, हमें 9 मिलता है। हम अपने उत्तर के दसवें हिस्से में संख्या 9 लिखते हैं:

अब सारे भाग 2+3=5 डाल दें। हम अपने उत्तर के पूर्णांक भाग में संख्या 5 लिखते हैं:

उत्तर मिला 5.92। अतः व्यंजक 2.65 + 3.27 का मान 5.92 . है

2,65 + 3,27 = 5,92

उदाहरण 4व्यंजक 9.5 + 2.8 . का मान ज्ञात कीजिए

इस व्यंजक को एक कॉलम में लिखें

हम भिन्नात्मक भाग 5 + 8 = 13 जोड़ते हैं। संख्या 13 हमारे उत्तर के भिन्नात्मक भाग में फिट नहीं होगी, इसलिए हम पहले संख्या 3 लिखते हैं, और इकाई को अगले अंक में स्थानांतरित करते हैं, या इसे पूर्णांक में स्थानांतरित करते हैं। अंश:

अब हम पूर्णांक भागों को जोड़ते हैं 9+2=11 प्लस इकाई जो हमें पिछले ऑपरेशन से मिली थी, हमें 12 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 12 लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 12.3. अतः व्यंजक 9.5 + 2.8 का मान 12.3 . है

9,5 + 2,8 = 12,3

दशमलव भिन्नों को जोड़ते समय, दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान होनी चाहिए। यदि पर्याप्त अंक नहीं हैं, तो भिन्नात्मक भाग में ये स्थान शून्य से भरे हुए हैं।

उदाहरण 5. व्यंजक का मान ज्ञात कीजिए: 12.725 + 1.7

इस व्यंजक को एक कॉलम में लिखने से पहले, आइए दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान करें। दशमलव भिन्न 12.725 में दशमलव बिंदु के बाद तीन अंक होते हैं, जबकि भिन्न 1.7 में केवल एक होता है। तो 1.7 के अंत में आपको दो शून्य जोड़ने होंगे। तब हमें भिन्न 1,700 प्राप्त होता है। अब आप इस व्यंजक को एक कॉलम में लिख सकते हैं और गणना करना शुरू कर सकते हैं:

5+0=5 का हज़ारवाँ भाग जोड़ें। हम अपने उत्तर के हजारवें भाग में 5 अंक लिखते हैं:

2+0=2 का सौवां भाग जोड़ें। हम अपने उत्तर के सौवें भाग में संख्या 2 लिखते हैं:

7+7=14 का दसवां हिस्सा जोड़ें। संख्या 14 हमारे उत्तर के दसवें हिस्से में फिट नहीं होगी। इसलिए, हम पहले संख्या 4 लिखते हैं, और इकाई को अगले बिट में स्थानांतरित करते हैं:

अब हम पूर्णांक भागों को जोड़ते हैं 12+1=13 प्लस इकाई जो हमें पिछले ऑपरेशन से मिली थी, हमें 14 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 14 लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 14,425। अतः व्यंजक का मान 12.725+1.700 है 14.425

12,725+ 1,700 = 14,425

दशमलव का घटाव

दशमलव अंशों को घटाते समय, आपको उन्हीं नियमों का पालन करना चाहिए जो जोड़ते समय: "अल्पविराम के तहत अल्पविराम" और "दशमलव बिंदु के बाद अंकों की समान संख्या"।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए 2.5 - 2.2

हम इस अभिव्यक्ति को "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं:

हम भिन्नात्मक भाग 5−2=3 की गणना करते हैं। हम अपने उत्तर के दसवें भाग में संख्या 3 लिखते हैं:

पूर्णांक भाग 2−2=0 की गणना करें। हम अपने उत्तर के पूर्णांक भाग में शून्य लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

हमें उत्तर 0.3 मिला। तो व्यंजक 2.5 - 2.2 का मान 0.3 . के बराबर है

2,5 − 2,2 = 0,3

उदाहरण 2व्यंजक 7.353 - 3.1 . का मान ज्ञात कीजिए

इस अभिव्यक्ति में अलग राशिदशमलव बिंदु के बाद अंक। भिन्न 7.353 में दशमलव बिंदु के बाद तीन अंक होते हैं, और भिन्न 3.1 में केवल एक होता है। इसका अर्थ है कि भिन्न 3.1 में, दोनों भिन्नों में अंकों की संख्या समान बनाने के लिए अंत में दो शून्य जोड़े जाने चाहिए। तब हमें 3,100 मिलते हैं।

अब आप इस व्यंजक को एक कॉलम में लिख सकते हैं और इसकी गणना कर सकते हैं:

उत्तर मिला 4,253। अतः व्यंजक 7.353 - 3.1 का मान 4.253 . है

7,353 — 3,1 = 4,253

सामान्य संख्याओं की तरह, यदि घटाना असंभव हो जाता है, तो कभी-कभी आपको आसन्न बिट से एक उधार लेना होगा।

उदाहरण 3व्यंजक 3.46 - 2.39 . का मान ज्ञात कीजिए

6−9 का सौवां भाग घटाएं। संख्या 6 से संख्या 9 घटाएं नहीं। इसलिए, आपको आसन्न अंक से एक इकाई लेने की आवश्यकता है। पड़ोसी अंक से एक को उधार लेने के बाद, संख्या 6 संख्या 16 में बदल जाती है। अब हम 16−9=7 के सौवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के सौवें भाग में सात को लिखते हैं:

अब दसवां घटाएं। चूँकि हमने दहाई की श्रेणी में एक इकाई ली थी, वहाँ जो आंकड़ा था वह एक इकाई कम हो गया। दूसरे शब्दों में, दसवां स्थान अब संख्या 4 नहीं है, बल्कि संख्या 3 है। आइए 3−3=0 के दसवें हिस्से की गणना करें। हम अपने उत्तर के दसवें भाग में शून्य लिखते हैं:

अब पूर्णांक भागों 3−2=1 को घटाएं। हम इकाई को अपने उत्तर के पूर्णांक भाग में लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 1.07. तो व्यंजक का मान 3.46−2.39 1.07 . के बराबर है

3,46−2,39=1,07

उदाहरण 4. व्यंजक का मान ज्ञात कीजिए 3−1.2

यह उदाहरण एक पूर्णांक से दशमलव घटाता है। आइए इस व्यंजक को एक कॉलम में लिखें ताकि दशमलव भिन्न 1.23 का पूर्णांक भाग संख्या 3 . के अंतर्गत हो

अब दशमलव बिंदु के बाद अंकों की संख्या को समान बनाते हैं। ऐसा करने के लिए, संख्या 3 के बाद, अल्पविराम लगाएं और एक शून्य जोड़ें:

अब दहाई घटाएँ: 0−2। संख्या 2 को शून्य से न घटाएं। इसलिए, आपको आसन्न अंक से एक इकाई लेने की आवश्यकता है। आसन्न अंक से एक को उधार लेकर, 0 संख्या 10 में बदल जाता है। अब आप 10−2=8 के दसवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के दसवें भाग में आठ लिखते हैं:

अब पूरे भागों को घटा दें। पहले, संख्या 3 पूर्णांक में स्थित थी, लेकिन हमने इससे एक इकाई उधार ली थी। नतीजतन, यह संख्या 2 में बदल गया। इसलिए, हम 2 से 1 घटाते हैं। 2−1=1. हम इकाई को अपने उत्तर के पूर्णांक भाग में लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर 1.8 मिला। तो व्यंजक 3−1.2 का मान 1.8 . है

दशमलव गुणन

दशमलव को गुणा करना आसान और मजेदार भी है। दशमलवों को गुणा करने के लिए, आपको अल्पविरामों को अनदेखा करते हुए उन्हें नियमित संख्याओं की तरह गुणा करना होगा।

उत्तर प्राप्त करने के बाद, पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दोनों अंशों में दशमलव बिंदु के बाद अंकों की संख्या गिनने की जरूरत है, फिर उत्तर में दाईं ओर समान अंकों की संख्या गिनें और अल्पविराम लगाएं।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए 2.5 × 1.5

हम इन दशमलव अंशों को अल्पविरामों को अनदेखा करते हुए साधारण संख्याओं के रूप में गुणा करते हैं। अल्पविराम को अनदेखा करने के लिए, आप अस्थायी रूप से कल्पना कर सकते हैं कि वे पूरी तरह से अनुपस्थित हैं:

हमें 375 मिले। इस संख्या में, पूरे भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद 2.5 और 1.5 के अंशों में अंकों की संख्या गिनने की आवश्यकता है। पहले भिन्न में दशमलव बिंदु के बाद एक अंक होता है, दूसरे भिन्न में भी एक होता है। कुल दो अंक।

हम 375 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 3.75। अतः व्यंजक 2.5 × 1.5 का मान 3.75 . है

2.5 x 1.5 = 3.75

उदाहरण 2व्यंजक का मान ज्ञात कीजिए 12.85 × 2.7

आइए अल्पविरामों को अनदेखा करते हुए इन दशमलवों को गुणा करें:

हमें 34695 मिले। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको 12.85 और 2.7 के अंशों में दशमलव बिंदु के बाद अंकों की संख्या की गणना करने की आवश्यकता है। अंश 12.85 में दशमलव बिंदु के बाद दो अंक होते हैं, अंश 2.7 में एक अंक होता है - कुल तीन अंक।

हम 34695 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 34,695। अतः व्यंजक 12.85 × 2.7 का मान 34.695 . है

12.85 x 2.7 = 34.695

एक दशमलव को एक नियमित संख्या से गुणा करना

कभी-कभी ऐसी स्थितियां होती हैं जब आपको एक दशमलव अंश को एक नियमित संख्या से गुणा करने की आवश्यकता होती है।

एक दशमलव और एक साधारण संख्या को गुणा करने के लिए, आपको दशमलव में अल्पविराम की परवाह किए बिना उन्हें गुणा करना होगा। उत्तर प्राप्त करने के बाद, पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दशमलव अंश में दशमलव बिंदु के बाद अंकों की संख्या की गणना करने की आवश्यकता है, फिर उत्तर में समान अंकों की संख्या को दाईं ओर गिनें और अल्पविराम लगाएं।

उदाहरण के लिए, 2.54 को 2 . से गुणा करें

हम अल्पविराम को अनदेखा करते हुए दशमलव अंश 2.54 को सामान्य संख्या 2 से गुणा करते हैं:

हमें संख्या 508 मिली है। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद अंश 2.54 में अंकों की संख्या गिनने की आवश्यकता है। भिन्न 2.54 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम 508 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 5.08. अतः व्यंजक 2.54 × 2 का मान 5.08 . है

2.54 x 2 = 5.08

दशमलव को 10, 100, 1000 . से गुणा करना

दशमलव को 10, 100, या 1000 से गुणा करना उसी तरह किया जाता है जैसे दशमलव को नियमित संख्याओं से गुणा करना। दशमलव अंश में अल्पविराम को अनदेखा करते हुए गुणा करना आवश्यक है, फिर उत्तर में, पूर्णांक भाग को भिन्नात्मक भाग से अलग करें, दाईं ओर अंकों की समान संख्या गिनें क्योंकि दशमलव में दशमलव बिंदु के बाद अंक थे अंश।

उदाहरण के लिए, 2.88 को 10 . से गुणा करें

आइए दशमलव भिन्न में अल्पविराम को अनदेखा करते हुए दशमलव भिन्न 2.88 को 10 से गुणा करें:

हमें 2880 मिले। इस संख्या में, आपको अल्पविराम से पूरे भाग को भिन्नात्मक भाग से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद अंश 2.88 में अंकों की संख्या गिनने की आवश्यकता है। हम देखते हैं कि भिन्न 2.88 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 2880 पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 28.80। हम अंतिम शून्य को छोड़ देते हैं - हमें 28.8.8.8 मिलता है। अतः व्यंजक 2.88 × 10 का मान 28.8 . है

2.88 x 10 = 28.8

दशमलव भिन्नों को 10, 100, 1000 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। यह इस तथ्य में समाहित है कि दशमलव अंश में अल्पविराम दाईं ओर उतने ही अंकों से आगे बढ़ता है जितने गुणक में शून्य होते हैं।

उदाहरण के लिए, पिछले उदाहरण 2.88×10 को इस प्रकार हल करते हैं। कोई गणना दिए बिना, हम तुरंत कारक 10 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसका एक शून्य है। अब भिन्न 2.88 में हम दशमलव बिंदु को एक अंक से दाईं ओर ले जाते हैं, हमें 28.8 मिलता है।

2.88 x 10 = 28.8

आइए 2.88 को 100 से गुणा करने का प्रयास करें। हम तुरंत कारक 100 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसके दो शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को दो अंकों से दाहिनी ओर ले जाते हैं, हमें 288 . प्राप्त होता है

2.88 x 100 = 288

आइए 2.88 को 1000 से गुणा करने का प्रयास करें। हम तुरंत कारक 1000 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाते हैं। तीसरा अंक नहीं है, इसलिए हम एक और शून्य जोड़ते हैं। नतीजतन, हमें 2880 मिलते हैं।

2.88 x 1000 = 2880

दशमलव को 0.1 0.01 और 0.001 से गुणा करना

दशमलव को 0.1, 0.01 और 0.001 से गुणा करना उसी तरह काम करता है जैसे दशमलव को दशमलव से गुणा करना। सामान्य संख्याओं की तरह भिन्नों को गुणा करना और उत्तर में अल्पविराम लगाना आवश्यक है, दाईं ओर जितने अंक हैं, उतने ही अंकों की गणना दशमलव बिंदु के बाद दोनों भिन्नों में होती है।

उदाहरण के लिए, 3.25 को 0.1 . से गुणा करें

हम इन भिन्नों को सामान्य संख्याओं की तरह गुणा करते हैं, अल्पविरामों को अनदेखा करते हुए:

हमें 325 मिले। इस संख्या में, आपको अल्पविराम से पूरे भाग को भिन्नात्मक भाग से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद 3.25 और 0.1 के अंशों में अंकों की संख्या की गणना करने की आवश्यकता है। भिन्न 3.25 में दशमलव बिंदु के बाद दो अंक होते हैं, भिन्न 0.1 में एक अंक होता है। कुल तीन अंक।

हम 325 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है। तीन अंक गिनने के बाद, हम पाते हैं कि संख्याएँ समाप्त हो गई हैं। इस मामले में, आपको एक शून्य जोड़ने और अल्पविराम लगाने की आवश्यकता है:

हमें उत्तर 0.325 मिला। अतः व्यंजक 3.25 × 0.1 का मान 0.325 . है

3.25 x 0.1 = 0.325

दशमलव को 0.1, 0.01 और 0.001 से गुणा करने का दूसरा तरीका है। यह विधि बहुत आसान और अधिक सुविधाजनक है। यह इस तथ्य में समाहित है कि दशमलव अंश में अल्पविराम बाईं ओर उतने ही अंकों से आगे बढ़ता है जितने गुणक में शून्य होते हैं।

उदाहरण के लिए, पिछले उदाहरण 3.25 × 0.1 को इस प्रकार हल करते हैं। कोई गणना दिए बिना, हम तुरंत कारक 0.1 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसका एक शून्य है। अब भिन्न 3.25 में हम दशमलव बिंदु को एक अंक से बाईं ओर ले जाते हैं। अल्पविराम को एक अंक बाईं ओर ले जाने पर, हम देखते हैं कि तीनों से पहले कोई और अंक नहीं हैं। इस मामले में, एक शून्य जोड़ें और अल्पविराम लगाएं। नतीजतन, हमें 0.325 . मिलता है

3.25 x 0.1 = 0.325

आइए 3.25 को 0.01 से गुणा करने का प्रयास करें। 0.01 के गुणक को तुरंत देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसके दो शून्य हैं। अब भिन्न 3.25 में हम अल्पविराम को बाईं ओर दो अंकों से घुमाते हैं, हमें 0.0325 . मिलता है

3.25 x 0.01 = 0.0325

आइए 3.25 को 0.001 से गुणा करने का प्रयास करें। 0.001 के गुणक को तुरंत देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को तीन अंकों से बाईं ओर ले जाते हैं, हमें 0.00325 . मिलता है

3.25 × 0.001 = 0.00325

दशमलव को 0.1, 0.001 और 0.001 से गुणा करके 10, 100, 1000 से गुणा करने में भ्रमित न हों। अधिकांश लोग एक सामान्य गलती करते हैं।

जब 10, 100, 1000 से गुणा किया जाता है, तो अल्पविराम को उतने अंकों से दाईं ओर ले जाया जाता है, जितने गुणक में शून्य होते हैं।

और जब 0.1, 0.01 और 0.001 से गुणा किया जाता है, तो अल्पविराम बाईं ओर उतने अंकों से चला जाता है जितने गुणक में शून्य होते हैं।

यदि पहली बार में यह याद रखना मुश्किल है, तो आप पहली विधि का उपयोग कर सकते हैं, जिसमें सामान्य संख्याओं के साथ गुणा किया जाता है। उत्तर में, आपको दाहिनी ओर जितने अंक हैं उतने अंकों की गणना करके पूर्णांक भाग को भिन्नात्मक भाग से अलग करना होगा क्योंकि दोनों अंशों में दशमलव बिंदु के बाद अंक होते हैं।

छोटी संख्या को बड़ी संख्या से विभाजित करना। अग्रवर्ती स्तर।

पिछले पाठों में से एक में, हमने कहा था कि छोटी संख्या को बड़ी संख्या से विभाजित करने पर एक भिन्न प्राप्त होता है, जिसके अंश में भाज्य होता है और हर में भाजक होता है।

उदाहरण के लिए, एक सेब को दो में विभाजित करने के लिए, आपको अंश में 1 (एक सेब) लिखना होगा, और हर में 2 (दो मित्र) लिखना होगा। परिणाम एक अंश है। तो प्रत्येक मित्र को एक सेब मिलेगा। दूसरे शब्दों में, आधा सेब। एक अंश एक समस्या का उत्तर है एक सेब को दो के बीच कैसे विभाजित करें

यह पता चला है कि यदि आप 1 को 2 से विभाजित करते हैं तो आप इस समस्या को और हल कर सकते हैं। आखिरकार, किसी भी भिन्न में एक भिन्नात्मक बार का अर्थ है विभाजन, जिसका अर्थ है कि इस विभाजन को एक अंश में भी अनुमति है। पर कैसे? हम इस तथ्य के अभ्यस्त हैं कि लाभांश हमेशा भाजक से अधिक होता है। और यहाँ, इसके विपरीत, लाभांश भाजक से कम है।

सब कुछ स्पष्ट हो जाएगा यदि हम याद रखें कि अंश का अर्थ है कुचलना, विभाजित करना, विभाजित करना। इसका अर्थ है कि इकाई को आप जितने चाहें उतने भागों में विभाजित किया जा सकता है, न कि केवल दो भागों में।

छोटी संख्या को बड़ी संख्या से भाग देने पर एक दशमलव भिन्न प्राप्त होता है, जिसमें पूर्णांक भाग 0 (शून्य) होगा। भिन्नात्मक भाग कुछ भी हो सकता है।

तो, आइए 1 को 2 से भाग दें। आइए इस उदाहरण को एक कोने से हल करते हैं:

एक को ऐसे ही दो भागों में विभाजित नहीं किया जा सकता। यदि आप एक प्रश्न पूछते हैं "एक में कितने दो होते हैं" , तो उत्तर 0 होगा। इसलिए, निजी तौर पर हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब, हमेशा की तरह, हम भागफल को भाजक से गुणा करके शेषफल निकालते हैं:

वह क्षण आ गया है जब इकाई को दो भागों में विभाजित किया जा सकता है। ऐसा करने के लिए, प्राप्त एक के दाईं ओर एक और शून्य जोड़ें:

हमें 10 मिला। हम 10 को 2 से भाग देते हैं, हमें 5 मिलता है। हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम गणना को पूरा करने के लिए अंतिम शेषफल निकालते हैं। 5 को 2 से गुणा करने पर हमें 10 . प्राप्त होता है

हमें उत्तर 0.5 मिला। तो भिन्न 0.5 . है

दशमलव भिन्न 0.5 का उपयोग करके आधा सेब भी लिखा जा सकता है। यदि हम इन दो हिस्सों (0.5 और 0.5) को जोड़ते हैं, तो हमें फिर से मूल एक पूरा सेब मिलता है:

इस बिंदु को भी समझा जा सकता है यदि हम कल्पना करें कि 1 सेमी को दो भागों में कैसे विभाजित किया जाता है। यदि आप 1 सेंटीमीटर को 2 भागों में विभाजित करते हैं, तो आपको 0.5 सेमी . मिलता है

उदाहरण 2व्यंजक 4:5 . का मान ज्ञात कीजिए

चार में कितने फाइव होते हैं? बिल्कुल भी नहीं। हम निजी 0 में लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम चार के नीचे शून्य लिखते हैं। इस शून्य को लाभांश से तुरंत घटाएं:

आइए अब चारों को 5 भागों में विभाजित (विभाजित) करना शुरू करते हैं। ऐसा करने के लिए, 4 के दाईं ओर, हम शून्य जोड़ते हैं और 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम आठ को निजी में लिखते हैं।

हम 8 को 5 से गुणा करके उदाहरण को पूरा करते हैं, और 40 प्राप्त करते हैं:

हमें उत्तर 0.8 मिला। अतः व्यंजक 4:5 का मान 0.8 . है

उदाहरण 3व्यंजक 5: 125 . का मान ज्ञात कीजिए

पांच में 125 कितनी संख्याएं हैं? बिल्कुल भी नहीं। हम निजी में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम पांच के नीचे 0 लिखते हैं। पांच 0 . में से तुरंत घटाएं

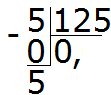
अब पांचों को 125 भागों में विभाजित (विभाजित) करते हैं। ऐसा करने के लिए, इस पाँच के दाईं ओर, हम शून्य लिखते हैं:

50 को 125 से विभाजित करें। 50 में 125 कितनी संख्याएँ हैं? बिल्कुल भी नहीं। अतः भागफल में हम पुनः 0 . लिखते हैं

हम 0 को 125 से गुणा करते हैं, हमें 0 मिलता है। हम इस शून्य को 50 के नीचे लिखते हैं। 50 . में से तुरंत 0 घटाएं

अब हम संख्या 50 को 125 भागों में विभाजित करते हैं। ऐसा करने के लिए, 50 के दाईं ओर, हम एक और शून्य लिखते हैं:

500 को 125 से विभाजित करें। 500 की संख्या में 125 कितनी संख्याएँ हैं। 500 की संख्या में चार संख्याएँ 125 हैं। हम चार को निजी में लिखते हैं:

हम 4 को 125 से गुणा करके उदाहरण को पूरा करते हैं, और 500 . प्राप्त करते हैं

हमें उत्तर 0.04 मिला। अतः व्यंजक 5: 125 का मान 0.04 . है

शेषफल के बिना संख्याओं का विभाजन

तो, आइए इकाई के बाद भागफल में अल्पविराम लगाते हैं, जिससे यह संकेत मिलता है कि पूर्णांक भागों का विभाजन समाप्त हो गया है और हम भिन्नात्मक भाग पर आगे बढ़ते हैं:

शेष 4 . में शून्य जोड़ें

अब हम 40 को 5 से भाग देते हैं, हमें 8 मिलता है। हम आठ को अकेले में लिखते हैं:

40−40=0. शेष में 0 प्राप्त किया। तो विभाजन पूरी तरह से पूरा हो गया है। 9 को 5 से भाग देने पर 1.8 का दशमलव प्राप्त होता है:

9: 5 = 1,8

उदाहरण 2. शेषफल के बिना 84 को 5 से भाग दें

पहले हम शेषफल के साथ हमेशा की तरह 84 को 5 से विभाजित करते हैं:

शेष में निजी 16 और 4 और प्राप्त हुए। अब हम इस शेषफल को 5 से विभाजित करते हैं। हम निजी क्षेत्र में अल्पविराम लगाते हैं, और शेष 4 . में 0 जोड़ते हैं

अब हम 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम दशमलव बिंदु के बाद भागफल में आठ लिखते हैं:

और यह जाँच कर उदाहरण पूरा करें कि क्या अभी भी शेष है:

एक दशमलव को एक नियमित संख्या से विभाजित करना

एक दशमलव भिन्न, जैसा कि हम जानते हैं, एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव अंश को एक नियमित संख्या से विभाजित करते समय, सबसे पहले आपको चाहिए:

• दशमलव अंश के पूर्णांक भाग को इस संख्या से विभाजित करें;
• पूर्णांक भाग विभाजित होने के बाद, आपको तुरंत निजी भाग में अल्पविराम लगाने और सामान्य विभाजन की तरह गणना जारी रखने की आवश्यकता है।

उदाहरण के लिए, आइए 4.8 को 2 . से भाग दें

आइए इस उदाहरण को एक कोने के रूप में लिखें:

अब हम पूरे भाग को 2 से भाग करते हैं। चार को दो से विभाजित करते हैं। हम ड्यूस को निजी तौर पर लिखते हैं और तुरंत अल्पविराम लगाते हैं:

अब हम भागफल को भाजक से गुणा करते हैं और देखते हैं कि क्या भाग से कोई शेष बचता है:

4−4=0. शेष शून्य है। हम अभी तक शून्य नहीं लिखते हैं, क्योंकि हल पूरा नहीं हुआ है। फिर हम गणना करना जारी रखते हैं, जैसा कि साधारण विभाजन में होता है। 8 नीचे लें और इसे 2 . से विभाजित करें

8: 2 = 4. हम चार को भागफल में लिखते हैं और भाजक से तुरंत गुणा करते हैं:

उत्तर 2.4 मिला। व्यंजक मान 4.8: 2 बराबर 2.4

उदाहरण 2व्यंजक का मान ज्ञात कीजिए 8.43:3

हम 8 को 3 से विभाजित करते हैं, हमें 2 मिलता है। दोनों के तुरंत बाद अल्पविराम लगाएं:

अब हम भागफल को भाजक 2 × 3 = 6 से गुणा करते हैं। हम छह को आठ के नीचे लिखते हैं और शेषफल पाते हैं:

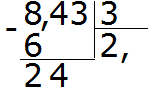
हम 24 को 3 से भाग देते हैं, हमें 8 मिलता है। हम आठ को अकेले में लिखते हैं। हम भाग के शेष को खोजने के लिए इसे तुरंत भाजक से गुणा करते हैं:

24−24=0. शेष शून्य है। शून्य अभी तक दर्ज नहीं किया गया है। लाभांश के अंतिम तीन लें और 3 से विभाजित करें, हमें 1 मिलता है। इस उदाहरण को पूरा करने के लिए तुरंत 1 को 3 से गुणा करें:

उत्तर 2.81 मिला। अतः व्यंजक 8.43: 3 का मान 2.81 . के बराबर है

दशमलव को दशमलव से भाग देना

दशमलव भिन्न को दशमलव भिन्न में विभाजित करने के लिए, लाभांश में और भाजक में, अल्पविराम को अंकों की उतनी ही संख्या से दाईं ओर ले जाएँ जितने कि भाजक में दशमलव बिंदु के बाद होते हैं, और फिर एक नियमित संख्या से विभाजित करते हैं।

उदाहरण के लिए, 5.95 को 1.7 . से भाग दें

आइए इस व्यंजक को एक कोने के रूप में लिखें

अब, भाजक में और भाजक में, हम अल्पविराम को दाईं ओर उतने ही अंकों से ले जाते हैं जितने कि भाजक में दशमलव बिंदु के बाद होते हैं। भाजक का दशमलव बिंदु के बाद एक अंक होता है। इसलिए हमें लाभांश और भाजक में अल्पविराम को एक अंक से दाईं ओर ले जाना चाहिए। स्थानांतरण:

दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, दशमलव अंश 5.95 भिन्न 59.5 में बदल गया। और दशमलव अंश 1.7, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, सामान्य संख्या 17 में बदल गया। और हम पहले से ही जानते हैं कि दशमलव अंश को सामान्य संख्या से कैसे विभाजित किया जाए। आगे की गणना मुश्किल नहीं है:

विभाजन को सुविधाजनक बनाने के लिए अल्पविराम को दाईं ओर ले जाया जाता है। इसकी अनुमति इस तथ्य के कारण दी जाती है कि जब लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित किया जाता है, तो भागफल नहीं बदलता है। इसका क्या मतलब है?

यह में से एक है दिलचस्प विशेषताएंविभाजन। इसे निजी संपत्ति कहा जाता है। व्यंजक 9: 3 = 3 पर विचार करें। यदि इस व्यंजक में भाज्य और भाजक को एक ही संख्या से गुणा या भाग किया जाता है, तो भागफल 3 नहीं बदलेगा।

आइए भाज्य और भाजक को 2 से गुणा करें और देखें कि क्या होता है:

(9 × 2) : (3 × 2) = 18: 6 = 3

जैसा कि उदाहरण से देखा जा सकता है, भागफल नहीं बदला है।

यही बात तब होती है जब हम भाजक और भाजक में अल्पविराम लगाते हैं। पिछले उदाहरण में, जहां हमने 5.91 को 1.7 से विभाजित किया था, हमने लाभांश और भाजक में अल्पविराम को एक अंक दाईं ओर ले जाया था। अल्पविराम को स्थानांतरित करने के बाद, भिन्न 5.91 को भिन्न 59.1 में और भिन्न 1.7 को सामान्य संख्या 17 में परिवर्तित किया गया था।

वास्तव में, इस प्रक्रिया के अंदर, 10 से गुणा हुआ। यहाँ यह कैसा दिखता है:

5.91 × 10 = 59.1

इसलिए, भाजक में दशमलव बिंदु के बाद अंकों की संख्या इस बात पर निर्भर करती है कि भाजक और भाजक को किससे गुणा किया जाएगा। दूसरे शब्दों में, भाजक में दशमलव बिंदु के बाद अंकों की संख्या निर्धारित करेगी कि लाभांश में कितने अंक हैं और भाजक में अल्पविराम को दाईं ओर ले जाया जाएगा।

दशमलव भाग 10, 100, 1000

दशमलव को 10, 100, या 1000 से विभाजित करना उसी तरह किया जाता है जैसे . उदाहरण के लिए, आइए 2.1 को 10 से भाग दें। आइए इस उदाहरण को एक कोने से हल करें:

लेकिन एक दूसरा तरीका भी है। यह हल्का है। इस पद्धति का सार यह है कि भाजक में अल्पविराम को बाईं ओर उतने अंकों से स्थानांतरित किया जाता है जितने कि भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस तरह हल करें। 2.1:10. हम डिवाइडर को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर एक अंक से स्थानांतरित करने की आवश्यकता है। हम अल्पविराम को एक अंक से बाईं ओर ले जाते हैं और देखते हैं कि कोई और अंक नहीं बचा है। इस मामले में, हम संख्या से पहले एक और शून्य जोड़ते हैं। नतीजतन, हमें 0.21 . मिलता है

आइए 2.1 को 100 से विभाजित करने का प्रयास करें। 100 की संख्या में दो शून्य होते हैं। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर दो अंकों से स्थानांतरित करने की आवश्यकता है:

2,1: 100 = 0,021

आइए 2.1 को 1000 से विभाजित करने का प्रयास करें। 1000 की संख्या में तीन शून्य होते हैं। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर तीन अंकों से स्थानांतरित करने की आवश्यकता है:

2,1: 1000 = 0,0021

दशमलव विभाजन 0.1, 0.01 और 0.001

दशमलव को 0.1, 0.01 और 0.001 से विभाजित करना उसी तरह किया जाता है जैसे . लाभांश और भाजक में, आपको अल्पविराम को दाईं ओर उतने अंकों से स्थानांतरित करने की आवश्यकता होती है जितने कि भाजक में दशमलव बिंदु के बाद होते हैं।

उदाहरण के लिए, आइए 6.3 को 0.1 से भाग दें। सबसे पहले, हम भाज्य में और भाजक में दायीं ओर उतने ही अंकों से अल्पविराम लगाते हैं जितने कि भाजक में दशमलव बिंदु के बाद होते हैं। भाजक का दशमलव बिंदु के बाद एक अंक होता है। इसलिए हम लाभांश में अल्पविराम और भाजक को एक अंक से दाईं ओर ले जाते हैं।

दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, दशमलव अंश 6.3 सामान्य संख्या 63 में बदल जाता है, और दशमलव अंश 0.1, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, एक में बदल जाता है। और 63 को 1 से विभाजित करना बहुत आसान है:

तो व्यंजक 6.3:0.1 का मान 63 . के बराबर है

लेकिन एक दूसरा तरीका भी है। यह हल्का है। इस पद्धति का सार यह है कि लाभांश में अल्पविराम को दाईं ओर उतने अंकों से स्थानांतरित किया जाता है जितने कि भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस तरह हल करें। 6.3:0.1। आइए डिवाइडर को देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। तो विभाज्य 6.3 में, आपको अल्पविराम को एक अंक से दाईं ओर ले जाने की आवश्यकता है। हम अल्पविराम को एक अंक से दाईं ओर ले जाते हैं और 63 . प्राप्त करते हैं

आइए 6.3 को 0.01 से भाग देने का प्रयास करें। भाजक 0.01 में दो शून्य होते हैं। तो विभाज्य 6.3 में, आपको अल्पविराम को दो अंकों से दाईं ओर ले जाने की आवश्यकता है। लेकिन लाभांश में दशमलव बिंदु के बाद केवल एक अंक होता है। इस मामले में, अंत में एक और शून्य जोड़ा जाना चाहिए। परिणामस्वरूप, हमें 630 . प्राप्त होता है

आइए 6.3 को 0.001 से विभाजित करने का प्रयास करें। 0.001 के भाजक में तीन शून्य होते हैं। तो विभाज्य 6.3 में, आपको अल्पविराम को तीन अंकों से दाईं ओर ले जाने की आवश्यकता है:

6,3: 0,001 = 6300

स्वतंत्र समाधान के लिए कार्य

क्या आपको सबक पसंद आया?
हमारे नए Vkontakte समूह में शामिल हों और नए पाठों की सूचनाएं प्राप्त करना शुरू करें

पिछले पाठ में, हमने सीखा कि दशमलव भिन्नों को कैसे जोड़ना और घटाना है (पाठ "दशमलव भिन्नों को जोड़ना और घटाना")। उसी समय, उन्होंने मूल्यांकन किया कि सामान्य "दो-कहानी" अंशों की तुलना में गणना कितनी सरल है।

दुर्भाग्य से, दशमलव अंशों के गुणा और भाग के साथ, यह प्रभाव नहीं होता है। कुछ मामलों में, दशमलव अंकन भी इन कार्यों को जटिल बनाता है।

आइए एक नई परिभाषा के साथ शुरू करते हैं। हम उससे बहुत बार मिलेंगे, और न केवल इस पाठ में।

किसी संख्या का महत्वपूर्ण हिस्सा ट्रेलरों सहित पहले और अंतिम गैर-शून्य अंकों के बीच सब कुछ है। हम केवल संख्याओं के बारे में बात कर रहे हैं, दशमलव बिंदु को ध्यान में नहीं रखा जाता है।

किसी संख्या के सार्थक भाग में सम्मिलित अंक सार्थक अंक कहलाते हैं। उन्हें दोहराया जा सकता है और शून्य के बराबर भी हो सकता है।

उदाहरण के लिए, कई दशमलव भिन्नों पर विचार करें और उनके संगत महत्वपूर्ण भागों को लिखें:

1. 91.25 → 9125 (महत्वपूर्ण आंकड़े: 9; 1; 2; 5);
2. 0.008241 → 8241 (महत्वपूर्ण आंकड़े: 8; 2; 4; 1);
3. 15.0075 → 150075 (महत्वपूर्ण आंकड़े: 1; 5; 0; 0; 7; 5);
4. 0.0304 → 304 (महत्वपूर्ण आंकड़े: 3; 0; 4);
5. 3000 → 3 (महत्वपूर्ण आंकड़ाकेवल एक: 3)।

कृपया ध्यान दें: संख्या के महत्वपूर्ण भाग के अंदर शून्य कहीं नहीं जाता है। जब हमने दशमलव भिन्न को साधारण भिन्न में बदलना सीखा तो हमने पहले ही कुछ इसी तरह का सामना किया है (पाठ "दशमलव भिन्न" देखें)।

यह बिंदु बहुत महत्वपूर्ण है, और यहां इतनी बार त्रुटियां की जाती हैं कि मैं निकट भविष्य में इस विषय पर एक परीक्षण प्रकाशित करूंगा। अभ्यास करना सुनिश्चित करें! और हम, एक महत्वपूर्ण भाग की अवधारणा से लैस होकर, वास्तव में, पाठ के विषय पर आगे बढ़ेंगे।

दशमलव गुणन

गुणन संक्रिया में लगातार तीन चरण होते हैं:

1. प्रत्येक भिन्न के लिए महत्वपूर्ण भाग लिखिए। आपको दो साधारण पूर्णांक मिलेंगे - बिना किसी हर और दशमलव अंक के;
2. इन नंबरों को किसी भी सुविधाजनक तरीके से गुणा करें। सीधे, यदि संख्याएँ छोटी हैं, या किसी स्तंभ में हैं। हमें वांछित अंश का महत्वपूर्ण भाग मिलता है;
3. पता लगाएं कि संबंधित महत्वपूर्ण भाग प्राप्त करने के लिए दशमलव बिंदु को मूल भिन्नों में कहां और कितने अंकों से स्थानांतरित किया गया है। पिछले चरण में प्राप्त महत्वपूर्ण भाग पर रिवर्स शिफ्ट करें।

मैं आपको एक बार फिर याद दिला दूं कि महत्वपूर्ण भाग के किनारों पर शून्य को कभी भी ध्यान में नहीं रखा जाता है। इस नियम की उपेक्षा करने से त्रुटियाँ होती हैं।

1. 0.28 12.5;
2. 6.3 1.08;
3. 132.5 0.0034;
4. 0.0108 1600.5;
5. 5.25 10,000।

हम पहली अभिव्यक्ति के साथ काम करते हैं: 0.28 12.5।

1. आइए इस व्यंजक से संख्याओं के महत्वपूर्ण भागों को लिखें: 28 और 125;
2. उनका उत्पाद: 28 125 = 3500;
3. पहले गुणक में, दशमलव बिंदु को 2 अंक दाईं ओर (0.28 → 28) स्थानांतरित किया जाता है, और दूसरे में - एक और 1 अंक। कुल मिलाकर, तीन अंकों के बाईं ओर एक बदलाव की आवश्यकता है: 3500 → 3.500 = 3.5।

अब आइए व्यंजक 6.3 1.08 से निपटें।

1. आइए महत्वपूर्ण भागों को लिखें: 63 और 108;
2. उनका उत्पाद: 63 108 = 6804;
3. फिर से, दो शिफ्ट दाईं ओर: क्रमशः 2 और 1 अंकों से। कुल मिलाकर - फिर से 3 अंक दाईं ओर, इसलिए रिवर्स शिफ्ट बाईं ओर 3 अंक होगी: 6804 → 6.804। इस बार अंत में कोई शून्य नहीं है।

हमें तीसरी अभिव्यक्ति मिली: 132.5 0.0034।

1. महत्वपूर्ण भाग: 1325 और 34;
2. उनका उत्पाद: 1325 34 = 45,050;
3. पहले अंश में, दशमलव बिंदु 1 अंक से दाईं ओर जाता है, और दूसरे में - 4 तक। कुल: 5 दाईं ओर। हम 5 से बाईं ओर शिफ्ट करते हैं: 45050 → .45050 = 0.4505। शून्य को अंत में हटा दिया गया था, और सामने जोड़ा गया ताकि "नंगे" दशमलव बिंदु न छोड़ें।

निम्नलिखित अभिव्यक्ति: 0.0108 1600.5।

1. हम महत्वपूर्ण भाग लिखते हैं: 108 और 16 005;
2. हम उन्हें गुणा करते हैं: 108 16 005 = 1 728 540;
3. हम दशमलव बिंदु के बाद संख्याओं की गणना करते हैं: पहली संख्या में 4 हैं, दूसरे में - 1. कुल - फिर से 5. हमारे पास: 1,728,540 → 17.28540 = 17.2854 है। अंत में, "अतिरिक्त" शून्य हटा दिया गया था।

अंत में, अंतिम अभिव्यक्ति: 5.25 10,000।

1. महत्वपूर्ण भाग: 525 और 1;
2. हम उन्हें गुणा करते हैं: 525 1 = 525;
3. पहली भिन्न को 2 अंकों को दाईं ओर स्थानांतरित किया जाता है, और दूसरे भिन्न को 4 अंकों को बाईं ओर स्थानांतरित किया जाता है (10,000 → 1.0000 = 1)। कुल 4 - 2 = 2 अंक बाईं ओर। हम 2 अंकों से दाईं ओर एक रिवर्स शिफ्ट करते हैं: 525, → 52 500 (हमें शून्य जोड़ना था)।

अंतिम उदाहरण पर ध्यान दें: चूंकि दशमलव बिंदु अलग-अलग दिशाओं में चलता है, कुल बदलाव अंतर के माध्यम से होता है। यह बहुत ही महत्वपूर्ण बिंदु! यहाँ एक और उदाहरण है:

1.5 और 12,500 की संख्या पर विचार करें। हमारे पास: 1.5 → 15 (1 से दाईं ओर शिफ्ट); 12 500 → 125 (2 को बाईं ओर शिफ्ट करें)। हम दाईं ओर 1 अंक और फिर बाईं ओर 2 अंक "कदम" करते हैं। परिणामस्वरूप, हमने बाईं ओर 2 - 1 = 1 अंक बढ़ा दिया।

दशमलव विभाजन

डिवीजन शायद सबसे कठिन ऑपरेशन है। बेशक, यहां आप गुणन के साथ सादृश्य द्वारा कार्य कर सकते हैं: महत्वपूर्ण भागों को विभाजित करें, और फिर दशमलव बिंदु को "स्थानांतरित करें"। लेकिन इस मामले में, कई सूक्ष्मताएं हैं जो संभावित बचत को नकारती हैं।

तो आइए एक सामान्य एल्गोरिथ्म को देखें जो थोड़ा लंबा है, लेकिन बहुत अधिक विश्वसनीय है:

1. सभी दशमलवों को उभयनिष्ठ भिन्नों में बदलें। थोड़े से अभ्यास के साथ, यह कदम आपको कुछ ही सेकंड में ले जाएगा;
2. परिणामी भिन्नों को विभाजित करें क्लासिक तरीका. दूसरे शब्दों में, पहले अंश को "उल्टे" दूसरे से गुणा करें (पाठ "संख्यात्मक अंशों का गुणा और भाग" देखें);
3. यदि संभव हो, तो परिणाम को दशमलव के रूप में लौटाएं। यह कदम भी तेज है, क्योंकि अक्सर हर में पहले से ही दस की शक्ति होती है।

एक कार्य। व्यंजक का मान ज्ञात कीजिए:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

हम पहली अभिव्यक्ति पर विचार करते हैं। सबसे पहले, आइए ओबी अंशों को दशमलव में बदलें:

हम दूसरी अभिव्यक्ति के साथ भी ऐसा ही करते हैं। पहले अंश का अंश फिर से कारकों में विघटित हो जाता है:

तीसरे और चौथे उदाहरण में एक महत्वपूर्ण बिंदु है: दशमलव अंकन से छुटकारा पाने के बाद, रद्द करने योग्य अंश दिखाई देते हैं। हालांकि, हम यह कटौती नहीं करेंगे।

अंतिम उदाहरण दिलचस्प है क्योंकि दूसरे अंश का अंश एक अभाज्य संख्या है। यहां कारक बनाने के लिए कुछ भी नहीं है, इसलिए हम इसे "रिक्त के माध्यम से" मानते हैं:

कभी-कभी विभाजन का परिणाम पूर्णांक में होता है (मैं अंतिम उदाहरण के बारे में बात कर रहा हूं)। इस मामले में, तीसरा चरण बिल्कुल नहीं किया जाता है।

इसके अलावा, विभाजित करते समय, "बदसूरत" अंश अक्सर दिखाई देते हैं जिन्हें दशमलव में परिवर्तित नहीं किया जा सकता है। यह वह जगह है जहां विभाजन गुणा से भिन्न होता है, जहां परिणाम हमेशा दशमलव रूप में व्यक्त किए जाते हैं। बेशक, ऐसे मामले में अंतिम चरणफिर से, यह पूरा नहीं हुआ है।

तीसरे और चौथे उदाहरण पर भी ध्यान दें। उनमें हम दशमलव से प्राप्त साधारण भिन्नों को जानबूझकर कम नहीं करते हैं। अन्यथा, यह व्युत्क्रम समस्या को जटिल बना देगा - अंतिम उत्तर को फिर से दशमलव रूप में प्रदर्शित करना।

याद रखें: एक भिन्न की मूल संपत्ति (गणित में किसी भी अन्य नियम की तरह) का अर्थ यह नहीं है कि इसे हर जगह और हमेशा, हर अवसर पर लागू किया जाना चाहिए।